
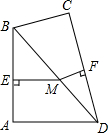
 如图所示,在四边形ABCD中,∠A=∠C=90°,M为BD上任一点,ME⊥AB于E,MF⊥CD于F,求证:$\frac{MF}{BC}$+$\frac{ME}{AD}$=1.
如图所示,在四边形ABCD中,∠A=∠C=90°,M为BD上任一点,ME⊥AB于E,MF⊥CD于F,求证:$\frac{MF}{BC}$+$\frac{ME}{AD}$=1. 分析 由EM∥AD,MF∥BC,推出$\frac{MF}{BC}$=$\frac{DM}{DB}$,$\frac{EM}{AD}$=$\frac{BM}{BD}$,两式相加即可证明.
解答 证明:∵ ∠A=∠C=90°,M为BD上任一点,ME⊥AB于E,MF⊥CD于F,
∠A=∠C=90°,M为BD上任一点,ME⊥AB于E,MF⊥CD于F,
∴∠BEM=∠A=90°,∠MFD=∠C=90°,
∴EM∥AD,MF∥BC,
∴$\frac{MF}{BC}$=$\frac{DM}{DB}$,$\frac{EM}{AD}$=$\frac{BM}{BD}$,
∴$\frac{MF}{BC}$+$\frac{ME}{AD}$=$\frac{DM}{DB}$+$\frac{BM}{BD}$=$\frac{DM+BM}{BD}$=$\frac{BD}{BD}$=1.
点评 本题考查相似三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是熟练应用平行线分线段成比例定理,属于中考常考题型.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=9没有实数根,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=9没有实数根,有下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=500}\\{(1+4%)x+(1+3%)y=500×(1+3.4)}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=500}\\{3%x+4%y=3.4%}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=500}\\{(1+3%)x+(1+4%)y=500×(1+3.4%)}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=500}\\{4%x+3%y=500×3.4%}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知点B的坐标为(10,0),点P(t,0)是OB上的一个动点,在x轴上方作等边△OPE和△BPF,连接EF,G为EF的中点.
如图,已知点B的坐标为(10,0),点P(t,0)是OB上的一个动点,在x轴上方作等边△OPE和△BPF,连接EF,G为EF的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计
某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计| 成绩x(分) | 频数 | 频率 |
| 50≤x<60 | 10 | a |
| 60≤x<70 | 16 | 0.08 |
| 70≤x<80 | b | 0.20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com