
【题目】一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:![]() )( )
)( )
A. 4.64海里 B. 5.49海里 C. 6.12海里 D. 6.21海里
【答案】B
【解析】
根据题意画出图如图所示:作BD⊥AC,取BE=CE,根据三角形内角和和等腰三角形的性质得出BA=BE,AD=DE,设BD=x,Rt△ABD中,根据勾股定理得AD=DE=![]() x,AB=BE=CE=2x,由AC=AD+DE+EC=2
x,AB=BE=CE=2x,由AC=AD+DE+EC=2![]() x+2x=30,解之即可得出答案.
x+2x=30,解之即可得出答案.
根据题意画出图如图所示:作BD⊥AC,取BE=CE,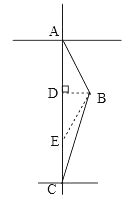
∵AC=30,∠CAB=30°∠ACB=15°,
∴∠ABC=135°,
又∵BE=CE,
∴∠ACB=∠EBC=15°,
∴∠ABE=120°,
又∵∠CAB=30°
∴BA=BE,AD=DE,
设BD=x,
在Rt△ABD中,
∴AD=DE=![]() x,AB=BE=CE=2x,
x,AB=BE=CE=2x,
∴AC=AD+DE+EC=2![]() x+2x=30,
x+2x=30,
∴x=![]() =
=![]() ≈5.49,
≈5.49,
故答案选:B.


科目:初中数学 来源: 题型:
【题目】如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知DE⊥EA,斜坡CD的长度为30m,DE的长为15m,则树AB的高度是_____m.
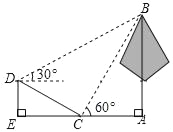
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图1,在平面直角坐标系xOy中,抛物线W的函数表达式为y=﹣![]() x2+
x2+![]() x+4.抛物线W与x轴交于A,B两点(点B在点A的右侧,与y轴交于点C,它的对称轴与x轴交于点D,直线l经过C、D两点.
x+4.抛物线W与x轴交于A,B两点(点B在点A的右侧,与y轴交于点C,它的对称轴与x轴交于点D,直线l经过C、D两点.
(1)求A、B两点的坐标及直线l的函数表达式.
(2)将抛物线W沿x轴向右平移得到抛物线W′,设抛物线W′的对称轴与直线l交于点F,当△ACF为直角三角形时,求点F的坐标,并直接写出此时抛物线W′的函数表达式.
(3)如图2,连接AC,CB,将△ACD沿x轴向右平移m个单位(0<m≤5),得到△A′C′D′.设A′C交直线l于点M,C′D′交CB于点N,连接CC′,MN.求四边形CMNC′的面积(用含m的代数式表示).
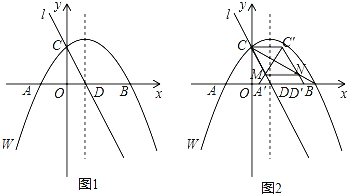
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小莉和哥哥玩扑克牌游戏,小莉有数字为1,2,3,5的四张牌,哥哥有数字为4,6,7,8的四张牌,按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,如果和为偶数,则小莉胜;如果和为奇数,则哥哥胜.
(1)请用数形图或列表法分别求出小莉胜和哥哥胜的概率;
(2)这个游戏公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
用户月用水量频数分布表 | ||
平均用水量(吨) | 频数 | 频率 |
3~6吨 | 10 | 0.1 |
6~9吨 | m | 0.2 |
9~12吨 | 36 | 0.36 |
12~15吨 | 25 | n |
15~18吨 | 9 | 0.09 |

请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=__ __,n=__ __;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
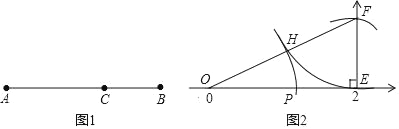
如图1,在线段AB上找一点C(AC>BC),若BC:AC=AC:AB,则称点C为线段AB的黄金分割点,这时比值为![]() ≈0.618,人们把
≈0.618,人们把![]() 称为黄金分割数.长期以来,很多人都认为黄金分割数是一个很特别的数,我国著名数学家华罗庚先生所推广的优选法中,就有一种0.618法应用了黄金分割数.
称为黄金分割数.长期以来,很多人都认为黄金分割数是一个很特别的数,我国著名数学家华罗庚先生所推广的优选法中,就有一种0.618法应用了黄金分割数.
我们可以这样作图找到已知线段的黄金分割点:如图2,在数轴上点O表示数0,点E表示数2,过点E作EF⊥OE,且EF=![]() OE,连接OF;以F为圆心,EF为半径作弧,交OF于H;再以O为圆心,OH为半径作弧,交OE于点P,则点P就是线段OE的黄金分割点.
OE,连接OF;以F为圆心,EF为半径作弧,交OF于H;再以O为圆心,OH为半径作弧,交OE于点P,则点P就是线段OE的黄金分割点.
根据材料回答下列问题:(1)线段OP长为_____,点P在数轴上表示的数为_____;(2)在(1)中计算线段OP长的依据是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com