函数y＝－
x，y＝－
x＋4，y＝3－x的共同性质是
[ ]
A．它们的图像都不经过第二象限
B．它们的图像都不经过原点
C．函数y都随自变量x的增大而增大
D．函数y都随自变量x的增大而减小
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案科目：初中数学 来源：69领航·单元同步训练 八年级(上册) 数学(人教版) 题型：022
函数y＝－2x＋3的图象经过点(________，0)和点(3，________)；对于函数，当自变量x＝________时，y＝0，当x＝3时，y＝________．
查看答案和解析>>
科目：初中数学 来源：初中数学 三点一测丛书 八年级数学 下 （江苏版课标本） 江苏版 题型：044
一般地，如果函数y＝f(x)对于自变量取值范围内的任意x，都有f(－x)＝－f(x)f那么y＝f(x)就叫做奇函数；如果函数y＝f(x)对于自变量取值范围内的任意x，都有f(－x)＝f(x)，那么y＝f(x)就叫做偶函数．
例如：f(x)＝x3＋x．
当x取任意实数，
f(－x)＝(－x)3＋(－x)＝－x3－x＝－(x3＋x)
即f(－x)＝－f(x)
所以f(x)＝x3＋x为奇函数．
又如：f(x)＝|x|，
当x取任意实数时，f(－x)＝|－x|＝|x|＝f(x)，
即f(－x)＝f(x)
所以f(x)为偶函数．
问题：(1)下列函数：
①y＝x4；②y＝x2＋1；③y＝
；④y＝
；⑤y＝x＋
．
所有奇函数是________，所有偶函数是________(只填序号)；
(2)请你再分别写出一个奇函数，一个偶函数．
查看答案和解析>>
科目：初中数学 来源：伴你学·数学·九年级·下册 题型：022
在同一直角坐标系中作出函数y＝x2，y＝(x－2)2和y＝(x－2)2＋3的图象，然后根据图象填空：
抛物线y＝x2的顶点坐标是( )，对称轴是________，开口向________；
抛物线y＝(x－2)2的顶点坐标是( )，对称轴是________，开口向________；
抛物线y＝(x－2)2＋3的顶点坐标是( )，对称轴是________，开口向________．
可以发现，抛物线y＝(x－2)2，y＝(x－2)2＋3与抛物线y＝x2的形状、开口大小相同，只是抛物线的位置发生了变化．把抛物线y＝x2沿x轴向________平移________个单位即可得到抛物线y＝(x－2)2；把抛物线y＝(x－2)2沿y轴向________平移________个单位即可得到抛物线y＝(x－2)2＋3；也就是说，把抛物线y＝x2沿x轴向________平移________个单位，再沿y轴向________平移________个单位即可得到抛物线y＝(x－2)2＋3．
还可以发现，对于y＝x2，当x＜0时y的值随x值的增大而________，当x＞0时y的值随x值的增大而________；对于y＝k(x－2)2，当x＜2时，y的值随x值的增大而________，当x＞2时，y的值随x值的增大而________；对于y＝(x－2)2＋3，当x＜2时，y的值随x值的增大而________，当x＞2时，y的值随x值的增大而________．
查看答案和解析>>
科目：初中数学 来源：新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型：044
如图所示，在直角坐标系内，O为坐标原点，A点坐标为(1，0)，点B在x轴上且在点A的右侧，AB＝AO，过点A和B作x轴的垂线分别交二次函数y＝x2的图象于C和D．直线OC交BD于点M，直线CD交y轴于点H，记点C，D的横坐标分别为xC，xD，点H的纵坐标为yH，同学发现两个结论：
①S△CDM∶S梯形ABMC＝2∶3；②数值相等关系xC·xD＝－yH．
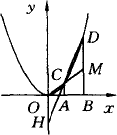
(1)请你验证结论①和②成立；
(2)请你研究：如果将上述题中的条件“A点坐标为(1，0)”改为“A(t，0)(t＞0)”，其他条件不变，结论①是否仍成立？
(3)进一步研究：如果将上述题中的条件A(1，0)改为A(t，0)(t＞0)，又将条件“y＝x2”改为“y＝ax2(a＞0)”，又将条件“y＝x2”改为“y＝ax2(a＞0)”其他条件不变，那么xC，xD和yH有怎样的数值关系？(写出结果并说明理由)
查看答案和解析>>
科目：初中数学 来源： 题型：
反比例函数y＝
的图象是轴对称图形，它的一条对称轴是下列哪个正比例函数的图象（ ）（改编）
A y＝|k|x B y＝－kx C y＝kx D y＝
x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
x图象过原点，y随x的增大而减小.函数y＝－
x＋4图象不过原点，过一、二、四象限，y随x的增大而减小，函数y＝3－x图象不过原点，过一、二、四象限，y随x的增大而减小，
