
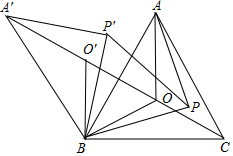
 如图,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点;△A′BO′、△A′BP′分别由△AOB、△APB逆时针旋转而得,旋转角都为60°,则下列结论:
如图,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点;△A′BO′、△A′BP′分别由△AOB、△APB逆时针旋转而得,旋转角都为60°,则下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由于△A′BO′,△A′BP′分别由△AOB,△APB旋转而得,旋转角都为60°,得到BO′=BO,BP′=BP,∠OBO′=∠PBP′=60°,∠A′O′B=∠AOB,O′A′=OA,P′A′=PA,则△BOO′和△BPP′都是等边三角形,得到∠BOO′=∠BO′O=60°,OO′=OB,而∠AOB=∠BOC=∠COA=120°,即可得到四个结论都正确.
解答 解:连PP′,如图,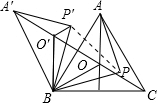
∵△A′BO′,△A′BP′分别由△AOB,△APB旋转而得,旋转角都为60°,
∴BO′=BO,BP′=BP,∠OBO′=∠PBP′=60°,∠A′O′B=∠AOB,O′A′=OA,P′A′=PA,
∴△BOO′和△BPP′都是等边三角形,
∴∠BOO′=∠BO′O=60°,OO′=OB,
∴A′O′+O′O=AO+BO,所以①正确;
而∠AOB=∠BOC=∠COA=120°,
∴∠A′O′O=∠O′OC=180°,
即△O′BO为等边三角形,且A′,O′,O,C在一条直线上,所以②正确;
A′P′+P′P=PA+PB,所以③正确;
又∵CP+PP′+P′A′>CA′=CO+OO′+O′A′,
∴PA+PB+PC>AO+BO+CO,所以④正确.
故选:D.
点评 本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了等边三角形的性质以及两点之间线段最短.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:填空题
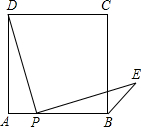 点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于45度.
点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于45度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.175×108元 | B. | 2.175×109元 | C. | 2.175×1010元 | D. | 2.175×1011元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 2 | 5 | 7 | 9 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com