
【题目】如图,平行四边形![]() .
.
(1)如图,点![]() 在
在![]() 延长线上,
延长线上,![]() ,求证:点
,求证:点![]() 为
为![]() 中点.
中点.

(2)如图,点![]() 在
在![]() 中点,
中点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,求证:
,求证:![]() .
.
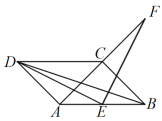
(3)在(2)的条件下,若![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,试判断四边形
,试判断四边形![]() 是否为平行四边形?并证明你的结论(先补全图形再解答).
是否为平行四边形?并证明你的结论(先补全图形再解答).

【答案】(1)见详解;(2)见详解;(3)四边形ACPE是平行四边形,补图与证明见详解.
【解析】
(1)先由平行四边形ABCD可得AD∥BC,AD=BC,再证四边形BDEC为平行四边形可得BC=DE,再等量代换即可得证;
(2)连接CE,根据三线合一可证得∠AEC=90°,结合∠DEF=90°,可得∠AED=∠CEF,根据∠ACB=90°,E为AB中点可得CE=AE,再结合∠DAE=∠ECF=135°即可证得△DAE≌△ECF进而得证;
(3)四边形ACPE是平行四边形,理由如下:先证得∠CEB=∠EBP=∠ECP=90°可得矩形BECP,进而得CP=BE等量代换得AE=CP,再结合AE∥CP即可得证.
证明:(1)∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∵AD∥BC,CE∥BD,
∴四边形BDEC为平行四边形,
∴BC=DE,
又∵AD=BC,
∴AD= DE,
∴点D为AE中点.
(2)如图,连接CE,
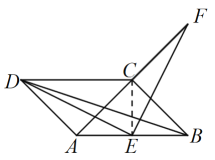
∵AD⊥AC,AD∥BC,
∴∠ACB=∠DAC=90°,
∵AD=BC,AD=AC,
∴BC=AC,
∵BC=AC,点E为AB中点,
∴CE⊥AB,
∴∠AEC=∠BEC=90°,
∴∠AED+∠DEC=90°,
∵ED⊥EF,
∴∠CEF+∠DEC=∠DEF=90°,
∴∠CEF=∠AED,
∵∠ACB=90°,BC=AC,
∴∠CAB=∠CBA=45°,
∴∠DAE=∠DAC+∠CAB=135°,
∵∠ACB=90°,点E为AB中点,
∴CE=AE=![]() AB,
AB,
∴∠ACE=∠CAB=45°,
∴∠FCE=180°-∠ACE=135°,
∴∠FCE=∠DAE,
在△DAE和△FCE中,
 ,
,
∴△DAE≌△FCE(ASA),
∴DE=EF.
(3)如图,

四边形ACPE是平行四边形,理由如下:
∵△DAE≌△FCE,
∴AD=CF,
∵AD=BC,
∴BC=CF,
又∵∠FCB=180°-∠ACB=90°,
∴∠CBF=∠CFB=45°,
∵∠CBA=45°,
∴∠EBF=∠CBF+∠CBA=90°,
∵AB∥CD,∠BEC=90°,
∴∠ECP=180°-∠BEC=90°,
∴∠ECP=∠BEC=∠EBF=90°,
∴四边形BECP为矩形,
∴BE=CP,
又∵AE=BE,
∴AE=CP,
∵AE=CP,AE∥CP,
∴四边形ACPE是平行四边形.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=(x-m)2-(x-m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=![]() .
.
①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某排球队6名上场队员的身高(单位:![]() )是:180,184,188,190,192,194,现用一名身高为
)是:180,184,188,190,192,194,现用一名身高为![]() 的队员换下场上身高为
的队员换下场上身高为![]() 的队员,与换人前相比,场上队员的身高平均数________.填“变大”.“不变”.“变小”),方差________.(填“变大”.“不变”.“变小”)
的队员,与换人前相比,场上队员的身高平均数________.填“变大”.“不变”.“变小”),方差________.(填“变大”.“不变”.“变小”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() ,点E在线段AB上,
,点E在线段AB上,![]() ,点F在直线AD上,
,点F在直线AD上,![]() .
.
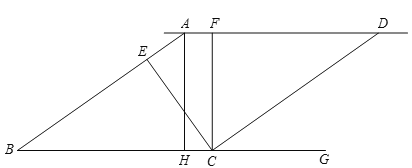
![]() 若
若![]() ,求
,求![]() 的度数;
的度数;
![]() 找出图中与
找出图中与![]() 相等的角,并说明理由;
相等的角,并说明理由;
![]() 在
在![]() 的条件下,点
的条件下,点![]() 不与点B、H重合
不与点B、H重合![]() 从点B出发,沿射线BG的方向移动,其他条件不变,请直接写出
从点B出发,沿射线BG的方向移动,其他条件不变,请直接写出![]() 的度数
的度数![]() 不必说明理由
不必说明理由![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
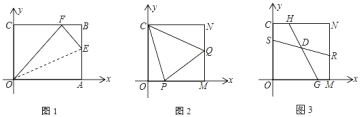
【题目】在平面直角坐标系xOy中,四边形OABC为矩形,OA在x轴正半轴上,OC在y轴正半轴上,且A(10,0)、C(0,8)
(1)如图1,在矩形OABC的边AB上取一点E,连接OE,将△AOE沿OE折叠,使点A恰好落在BC边上的F处,求AE的长;
(2)将矩形OABC的AB边沿x轴负方向平移至MN(其它边保持不变),M、N分别在边OA、CB上且满足CN=OM=OC=MN.如图2,P、Q分别为OM、MN上一点.若∠PCQ=45°,求证:PQ=OP+NQ;
(3)如图3,S、G、R、H分别为OC、OM、MN、NC上一点,SR、HG交于点D.若∠SDG=135°,HG=4![]() ,求RS的长.
,求RS的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,你我同行”.两年来,扬州市区的公共自行车给市民出行带来切实方便.电视台记者在某区街头随机选取了市民进行调查,调查的问题是“您大概多久使用一次公共自行车?”,将本次调查结果归为四种情况:A.每天都用;B.经常使用;C.偶尔使用;D.从未使用.将这次调查情况整理并绘制如下两幅统计图如图2:

根据图中的信息,解答下列问题:
(1)本次活动共有 位市民参与调查;
(2)补全条形统计图和扇形统计图;
(3)扇形统计图中A项所对应的圆心角的度数为
(4)根据统计结果,若该区有46万市民,请估算每天都用公共自行车的市民约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com