
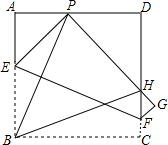
 如图,现有边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连结BP、BH.
如图,现有边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连结BP、BH.分析 (1)根据翻折变换的性质得出∠PBC=∠BPH,进而利用平行线的性质得出∠APB=∠PBC即可得出答案;
(2)首先设AE=x,则EP=4-x,由勾股定理可得:在Rt△AEP中,AE2+AP2=PE2,即可得方程:x2+12=(4-x)2,即可求得答案AE的长,易证得△DPH∽△AEP,然后由相似三角形的对应边成比例,求得答案;
(3)首先过B作BQ⊥PH,垂足为Q,易证得△ABP≌△QBP,进而得出△BCH≌△BQH,即可得出AP+HC=PH.
解答 (1)证明:∵PE=BE,
∴∠EPB=∠EBP,
又∵∠EPH=∠EBC=90°,
∴∠EPH-∠EPB=∠EBC-∠EBP.
即∠BPH=∠PBC.
又∵四边形ABCD为正方形
∴AD∥BC,
∴∠APB=∠PBC.
∴∠APB=∠BPH.
(2)解:∵AP=1,
∴PD=AD-AP=4-1=3,
设AE=x,则EP=4-x,
在Rt△AEP中,AE2+AP2=PE2,
即x2+12=(4-x)2,
解得:x=$\frac{15}{8}$,
∵∠A=∠D=∠ABC=90°,
∴∠AEP+∠APE=90°,
由折叠的性质可得:∠EPG=∠ABC=90°,
∴∠APE+∠DPH=90°,
∴∠AEP=∠DPH,
∴△DPH∽△AEP,
∴$\frac{DH}{AP}$=$\frac{DP}{AE}$,
∴$\frac{DH}{1}$=$\frac{3}{\frac{15}{8}}$,
解得:DH=$\frac{8}{5}$;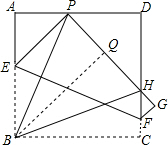
(3)证明:过B作BQ⊥PH,垂足为Q,
由(1)知,∠APB=∠BPH,
在△ABP与△QBP中,
$\left\{\begin{array}{l}{∠A=∠BQP=90°}\\{∠APB=∠BPH}\\{BP=BP}\end{array}\right.$,
∴△ABP≌△QBP(AAS),
∴AP=QP,BA=BQ.
又∵AB=BC,
∴BC=BQ.
又∵∠C=∠BQH=90°,
∴△BCH和△BQH是直角三角形,
在Rt△BCH与Rt△BQH中,
$\left\{\begin{array}{l}{BC=BQ}\\{BH=BH}\end{array}\right.$,
∴Rt△BCH≌Rt△BQH(HL),
∴CH=QH,
∴AP+HC=PH.
点评 此题属于四边形的综合题.考查了正方形的性质、折叠的性质、全等三角形的判定与性质、相似三角形的判定与性质以及勾股定理等知识.注意掌握折叠前后图形的对应关系、注意掌握方程思想的应用,注意准确作出辅助线是解此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | y=-7x+7 | B. | y=-7x+1 | C. | y=-7x-17 | D. | y=-7x+25 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某电脑公司销售部为了制订下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的平均数、中位数、众数分别是14.4,12,10.
某电脑公司销售部为了制订下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的平均数、中位数、众数分别是14.4,12,10.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将边长为$\sqrt{3}$cm的正方形ABCD绕点A逆时针方向旋转30°后得到正方形AB′C′D′,则图中阴影部分的面积为( )
如图,将边长为$\sqrt{3}$cm的正方形ABCD绕点A逆时针方向旋转30°后得到正方形AB′C′D′,则图中阴影部分的面积为( )| A. | $\frac{3}{4}$cm2 | B. | $\frac{3}{2}$cm2 | C. | $\sqrt{3}$cm2 | D. | (3-$\sqrt{3}$)cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 营业员 | 小王 | 小李 |
| 月销售件数 | 200 | 150 |
| 月总收入(单位:元) | 2500 | 2250 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售额/万元 | 29 | 32 | 34 | 38 | 48 | 55 |
| 专卖店/个数 | 1 | 1 | 3 | 2 | 2 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com