
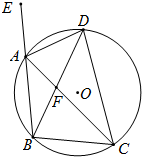
 如图,等腰△ABC内接于⊙O,AB=BC,它的外角∠EAC的平分线交⊙O于D点,DB交AC于F.
如图,等腰△ABC内接于⊙O,AB=BC,它的外角∠EAC的平分线交⊙O于D点,DB交AC于F.| 2 |
| 3 |
| DA |
| DB |
| 2 |
| 3 |
| 4 |
| 3 |
|
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| DA |
| DB |
| 1 |
| 3 |


科目:初中数学 来源: 题型:
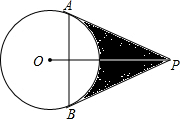 如图,已知PA,PB切⊙O于A、B两点,连AB,∠APB=60°AB=
如图,已知PA,PB切⊙O于A、B两点,连AB,∠APB=60°AB=| 3 |
 |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
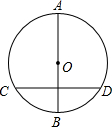 如图,在⊙O中AB为直径,CD为非直径的弦,(1)AB⊥CD;(2)AB平分CD;(3)AB平分CD所对的两条弧.若以(1)、(2)、(3)中的一个为条件,另两个为结论构成三个命题,其中真命题的个数为( )
如图,在⊙O中AB为直径,CD为非直径的弦,(1)AB⊥CD;(2)AB平分CD;(3)AB平分CD所对的两条弧.若以(1)、(2)、(3)中的一个为条件,另两个为结论构成三个命题,其中真命题的个数为( )| A、3 | B、2 | C、1 | D、0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
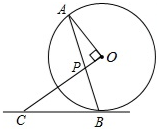 如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P.
如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P.| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 △ABC中,AB=AC,AD⊥BC于D,以AC为边在△ABC外作等边△ACE,连BE交AD于M;
△ABC中,AB=AC,AD⊥BC于D,以AC为边在△ABC外作等边△ACE,连BE交AD于M;| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 样式 | 颜色 | 做工 | 价格 | ||
| 甲 沙 发 | 爸爸 | 2 | 3 | 3 | 2 |
| 妈妈 | 3 | 2 | 4 | 3 | |
| 小明 | 4 | 1 | 3 | 3 | |
| 乙 沙 发 | 爸爸 | 2 | 4 | 3 | 4 |
| 妈妈 | 3 | 3 | 4 | 3 | |
| 小明 | 3 | 3 | 3 | 2 | |
| 丙 沙 发 | 爸爸 | 4 | 3 | 2 | 3 |
| 妈妈 | 3 | 4 | 2 | 3 | |
| 小明 | 4 | 2 | 2 | 2 | |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在一个矩形纸片ABCD剪上减去一个正方形ABEF,所余下的矩形ECDF于原矩形ABCD相似,那么原矩形中较长的边BC与较短的边AB的比是多少?
如图,在一个矩形纸片ABCD剪上减去一个正方形ABEF,所余下的矩形ECDF于原矩形ABCD相似,那么原矩形中较长的边BC与较短的边AB的比是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com