
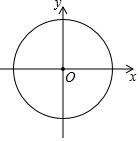
 在平面直角坐标系xOy中,⊙O的半径是5,点A为⊙O上一点,AB⊥x轴于点B,AC⊥y轴于点C,若四边形ABOC的面积为12,写出一个符合条件的点A的坐标(3,4).
在平面直角坐标系xOy中,⊙O的半径是5,点A为⊙O上一点,AB⊥x轴于点B,AC⊥y轴于点C,若四边形ABOC的面积为12,写出一个符合条件的点A的坐标(3,4). 分析 设点A坐标为(x,y),由圆的半径为5可得x2+y2=25,根据矩形的面积为xy=12或xy=-12,分情况分别解$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=25}\\{xy=12}\end{array}\right.$和$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=25}\\{xy=-12}\end{array}\right.$可得点A的坐标.
解答 解:设点A坐标为(x,y),
则AO2=x2+y2=25,
由xy=12或xy=-12,
当xy=12时,
可得(x+y)2-2xy=25,即(x+y)2-24=25,
∴x+y=7或x+y=-7,
①若x+y=7,即y=7-x,代入xy=12得x2-7x+12=0,
解得:x=3或x=4,
当x=3时,y=4;当x=4时,y=3;
即点A(3,4)或(4,3);
②若x+y=-7,则y=-7-x,代入xy=12得:x2+7x+12=0,
解得:x=-3或x=-4,
当x=-3时,y=-4;当x=-4时,y=-3;
即点A(-3,-4)或(-4,-3);
当xy=-12时,
可得(x+y)2-2xy=25,即(x+y)2+24=25,
∴x+y=1或x+y=-1,
③若x+y=1,即y=1-x,代入xy=-12得x2-x-12=0,
解得:x=-3或x=4,
当x=-3时,y=4;当x=4时,y=-3;
即点A(-3,4)或(4,-3);
④若x+y=-1,则y=-1-x,代入xy=-12得:x2+x-12=0,
解得:x=3或x=-4,
当x=3时,y=-4;当x=-4时,y=3;
即点A(3,-4)或(-4,3);
故答案为:(3,4),(答案不唯一).
点评 本题主要考查坐标与图形的性质,熟练掌握两点的距离公式和解二元二次方程组是解题的关键.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:选择题
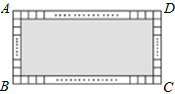 如图所示的是由一个小矩形与52个边长为1的小正方形组成的大矩形,小矩形的长与宽之比是7:5,若设小矩形的长为x,宽为y,则根据题意可列方程组( )
如图所示的是由一个小矩形与52个边长为1的小正方形组成的大矩形,小矩形的长与宽之比是7:5,若设小矩形的长为x,宽为y,则根据题意可列方程组( )| A. | $\left\{\begin{array}{l}{x:y=7:5}\\{2(x+y)+4=52}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x:y=5:7}\\{2(x+y)+4=52}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x:y=5:7}\\{x+y=52}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x:y=7:5}\\{2(x+y)=52}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,BO平分∠ABC,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=10,则△AMN的周长为( )
如图,BO平分∠ABC,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=10,则△AMN的周长为( )| A. | 22 | B. | 36 | C. | 46 | D. | 34 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com