
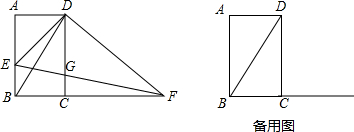
���� ��1������ƽ���ı��ε����ʵõ���A=��ADC=��DCB=90�㣬������ǵ����ʵõ���ADE=��CDF�������������ε��ж��������ɵõ����ۣ�
��2����ֱ�������εõ�CD=$\sqrt{3}$�����ݾ��ε����ʵõ�AD=BC=1��AB=CD=$\sqrt{3}$���������������ε����ʵõ�$\frac{DE}{DF}$=$\frac{\sqrt{3}}{3}$���������Ǻ����Ķ��弴�ɵõ����ۣ�
��3���ٸ������������ε����ʵõ�CF=3-$\sqrt{3}$x�����������ε������ʽ�õ������Ľ���ʽ�����ݶ��κ����Ķ������꼴�ɵõ����ۣ��ڸ��ݵ�xΪ$\frac{2\sqrt{3}}{3}$ʱ��y�����ֵ���õ�BE=$\frac{2\sqrt{3}}{3}$��CF=1��BF=2���������������ε���õ�CG=$\frac{\sqrt{3}}{3}$�����ǵõ�BE=DG������BE��DG�����ɵõ����ۣ�
��� �⣺��1���ھ���ABCD�У�
�ߡ�A=��ADC=��DCB=90�㣬
���A=��DCF=90�㣬
��DF��DE��
���A=��EDF=90�㣬
���ADE=��CDF��
���ADE�ס�CDF��
��2����BC=1����DBC=60�㣬
��CD=$\sqrt{3}$��
�ھ���ABCD�У�
��AD=BC=1��AB=CD=$\sqrt{3}$��
�ߡ�ADE�ס�CDF��
��$\frac{DE}{DF}=\frac{AD}{CD}$=$\frac{\sqrt{3}}{3}$��
��tan��DEF=$\frac{DF}{DE}$��
��$\frac{DF}{DE}$=$\sqrt{3}$��
���DEF=60�㣻
��3���١�BE=x��
��AE=$\sqrt{3}$-x��
�ߡ�ADE�ס�CDF��
��$\frac{AE}{CF}=\frac{AD}{CD}$=$\frac{\sqrt{3}}{3}$��
��CF=3-$\sqrt{3}$x��
��BF=BC+CF=4-$\sqrt{3}$x��
��y=$\frac{1}{2}$BE•BF=$\frac{1}{2}$x��4-$\sqrt{3}$x��=-$\frac{\sqrt{3}}{2}$x2+2x��
��y=-$\frac{\sqrt{3}}{2}$x2+2x=-$\frac{\sqrt{3}}{2}$��x-$\frac{2\sqrt{3}}{3}$��2+$\frac{2\sqrt{3}}{3}$��
�൱xΪ$\frac{2\sqrt{3}}{3}$ʱ��y�����ֵ��
��yΪ���ֵʱ����ʱ�ı���BGDE��ƽ���ı��Σ�
�ߵ�xΪ$\frac{2\sqrt{3}}{3}$ʱ��y�����ֵ��
��BE=$\frac{2\sqrt{3}}{3}$��CF=1��BF=2��
��CG��BE��
���CFG�ס�BFE��
��$\frac{CG}{BE}=\frac{CF}{BF}$��
��CG=$\frac{\sqrt{3}}{3}$��
��DG=$\frac{2\sqrt{3}}{3}$��
��BG=$\sqrt{{1}^{2}+��\frac{\sqrt{3}}{3}��^{2}}$=$\frac{2\sqrt{3}}{3}$��
��BE=DG=BG����BE��DG��
���ı���BGDE�����Σ�
���� ���⿼�������������ε��ж������ʣ������Ľ���ʽ�����κ��������ֵ��ƽ���ı��ε��ж������ε����ʣ������������������ε��ж��������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m=-7��n=3 | B�� | m=7��n=-3 | C�� | m=-7��n=-3 | D�� | m=7��n=3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
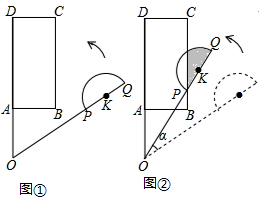 ƽ���ϣ�����ABCD��ֱ��ΪQP�İ�ԲK��ͼ��ͼ�ٰڷţ��ֱ��ӳ�DA��QP���ڵ�O���ҡ�DOQ=60�㣬OQ=OD=3��OP=2��OA=AB=1�����߶�OD������ABCDλ�ù̶������߶�OQ�����Ű�ԲKһ�����ŵ�O����ʱ�뿪ʼ��ת����ͼ�ڣ�����Pǡ������BC����ʱ��S��Ӱ=$\frac{��}{24}$+$\frac{\sqrt{3}}{16}$��
ƽ���ϣ�����ABCD��ֱ��ΪQP�İ�ԲK��ͼ��ͼ�ٰڷţ��ֱ��ӳ�DA��QP���ڵ�O���ҡ�DOQ=60�㣬OQ=OD=3��OP=2��OA=AB=1�����߶�OD������ABCDλ�ù̶������߶�OQ�����Ű�ԲKһ�����ŵ�O����ʱ�뿪ʼ��ת����ͼ�ڣ�����Pǡ������BC����ʱ��S��Ӱ=$\frac{��}{24}$+$\frac{\sqrt{3}}{16}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a0=1 | B�� | a-2=-a | C�� | ��-a��2=-a2 | D�� | ��ab��2=ab2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | 2 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�DE��BC���ֱ�AB��AC�ڵ�D��E����AD=4��DB=3��BC=9����DE�ij�Ϊ$\frac{36}{7}$��
��ͼ���ڡ�ABC�У�DE��BC���ֱ�AB��AC�ڵ�D��E����AD=4��DB=3��BC=9����DE�ij�Ϊ$\frac{36}{7}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ������ABC�Ƶ�A����ʱ����ת50��õ���ADC�䣬���ABD�Ķ����ǣ�������
��ͼ��ʾ������ABC�Ƶ�A����ʱ����ת50��õ���ADC�䣬���ABD�Ķ����ǣ�������| A�� | 30�� | B�� | 45�� | C�� | 65�� | D�� | 75�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��A��B����֮����һ��ɽ������ԭ����A�ص�B���뾭C��������A-C-B��ʻ��ȫ��68km���ֿ�ͨ����������ֱ����ֱ��AB��ʻ����֪��A=30�㣬��B=45�㣬��������ͨ��������A�ص�B�ر�ԭ�����߶���ǧ�ף��������ȷ��0.1km�����ο����ݣ�$\sqrt{2}$��1.4��$\sqrt{3}$��1.7��
��ͼ��A��B����֮����һ��ɽ������ԭ����A�ص�B���뾭C��������A-C-B��ʻ��ȫ��68km���ֿ�ͨ����������ֱ����ֱ��AB��ʻ����֪��A=30�㣬��B=45�㣬��������ͨ��������A�ص�B�ر�ԭ�����߶���ǧ�ף��������ȷ��0.1km�����ο����ݣ�$\sqrt{2}$��1.4��$\sqrt{3}$��1.7���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com