
【题目】随着中央电视台《朗读者》节目的播出,“朗读”为越来越多的同学所喜爱,西宁市某中学计划在全校开展“朗读”活动,为了了解同学们对这项活动的参与态度,随机对部分学生进行了一次调查,调查结果整理后,将这部分同学的态度划分为四个类别:![]() .积极参与,
.积极参与,![]() .一定参与,
.一定参与,![]() .可以参与,
.可以参与,![]() .不参与.根据调查结果制作了如下不完整的统计表和统计图.
.不参与.根据调查结果制作了如下不完整的统计表和统计图.
学生参与“朗读”的态度统计表
类别 | 人数 | 所占百分比 |
| 18 |
|
| 20 |
|
|
|
|
| 4 |
|
合计 |
|
|
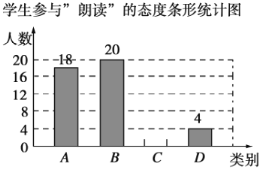
请你根据以上信息,解答下列问题:
(1)![]() ______,
______,![]() ______,并将条形统计图补充完整;
______,并将条形统计图补充完整;
(2)该校有1500名学生,如果“不参与”的人数不超过150人时,“朗读”活动可以顺利开展,通过计算分析这次活动能否顺利开展?
(3)“朗读”活动中,九年级一班比较优秀的四名同学恰好是两男两女,从中随机选取两人在班级进行朗读示范,试用画树状图法或列表法求所选两人都是女生的概率,并列出所有等可能的结果.
【答案】(1)![]() ,8,补图详见解析;(2)这次活动能顺利开展;(3)
,8,补图详见解析;(2)这次活动能顺利开展;(3)![]() (两人都是女生)
(两人都是女生)![]()
【解析】
(1)先用20除以40%求出样本容量,然后求出a, m的值,并补全条形统计图即可;
(2)先求出b的值,用b的值乘以1500,然后把计算的结果与150进行大小比较,则可判断这次活动能否顺利开展;
(3)画树状图展示所有12种等可能的结果数,找出所选两人都是女生的结果数为2,然后根据概率公式计算.
解:(1))20÷40%=50人,
a=18÷50×100%=36%,
m=50×16%=8,

(2)b=4÷50×100%=8%,![]() (人)
(人)
∵![]() ∴这次活动能顺利开展.
∴这次活动能顺利开展.
(3)树状图如下:

由此可见,共有12种等可能的结果,其中所选两人都是女生的结果数有2种
∴![]() (两人都是女生)
(两人都是女生)![]() .
.


科目:初中数学 来源: 题型:
【题目】某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
A型利润(元/件) | B型利润(元/件) | |
甲店 | 180 | 150 |
乙店 | 120 | 110 |
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并写出x的取值范围;
(2)若要求总利润超过14960元,有多少种不同分配方案?请列出具体方案;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润,甲店的B型产品以及乙店的A,B型产品的每件利润不变,该公司如何设计分配方案,使总利润达到最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某坦克部队需要经过一个拱桥(如图所示),拱桥的轮廓是抛物线形,拱高OC=6m,跨度AB=20m,有5根支柱:AG、MN、CD、EF、BH,相邻两支柱的距离均为5m.
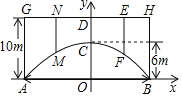
(1)以AB的中点为原点,AB所在直线为x轴,支柱CD所在直线为y轴,建立平面直角坐标系,求抛物线的解析式;
(2)若支柱每米造价为2万元,求5根支柱的总造价;
(3)拱桥下面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道是坦克的行进方向,现每辆坦克长4m,宽2m,高3m,行驶速度为24km/h,坦克允许并排行驶,坦克前后左右距离忽略不计,试问120辆该型号坦克从刚开始进入到全部通过这座长1000m的拱桥隧道所需最短时间为多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
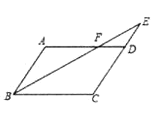
【题目】如图,在口ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= ![]() CD
CD
(1)求证:△ABF∽△CEB
(2)若△DEF的面积为2,求△CEB的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
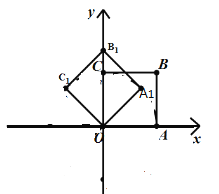
【题目】如图,在平面直角坐标系中,将正方形![]() 绕点
绕点![]() 逆时针旋转45°后得到正方形
逆时针旋转45°后得到正方形![]() .依此方式,绕点
.依此方式,绕点![]() 连续旋转2020次,得到正方形
连续旋转2020次,得到正方形![]() ,如果点
,如果点![]() 的坐标为
的坐标为![]() ,那么点
,那么点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
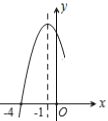
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③一元二次方程
;③一元二次方程![]() 的解是
的解是![]() ,
,![]() ;④当
;④当![]() 时,
时,![]() ,其中正确的结论有__________.
,其中正确的结论有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
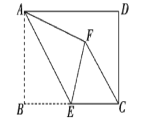
【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长度为_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com