
【题目】如图,将正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为FG.若BG=2cm,DE=3cm,则FG的长为_______.
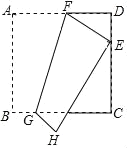
【答案】3![]()
【解析】
过点G作GQ⊥AD于Q,根据翻折变换的性质可得GF⊥AE,然后求出∠GFQ=∠D,再利用“角角边”证明△ADE和△GQF全等,根据全等三角形对应边相等可得GF=AE,再利用勾股定理列式求出AE,从而得解.
解:如图,过点G作GQ⊥AD于Q,则四边形ABGQ中,QG=AB,
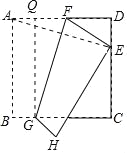
由翻折变换的性质得GF⊥AE,
∵∠AFG+∠DAE=90°,∠AED+∠DAE=90°,
∴∠AFG=∠AED,
∵四边形ABCD是正方形,
∴AD=AB,
∴QG=AD,
在△ADE和△GQF中,
 ,
,
∴△ADE≌△GQF(AAS),
∴GF=AE,
∵BG=2cm,DE=3cm,
∴AF=EF=AQ+QF=BG+DE=2+3=5,
在Rt△FDE中,DF=![]() ,
,
∴AD=AF+FD=5+4=9,
在Rt△ADE中,由勾股定理得,AE=![]() ,
,
∴GF的长为3![]() .
.
故答案为:3![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,∠ABD=∠ABC,补充一个条件,使得△ABD≌△ABC,则下列选项不符合题意的是( )
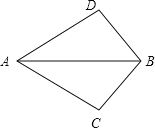
A. ∠D=∠CB. ∠DAB=∠CABC. BD=BCD. AD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组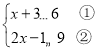 .请结合题意填空,完成本题的解答
.请结合题意填空,完成本题的解答
(Ⅰ)解不等式①,得__________;
(Ⅱ)解不等式②,得__________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2﹣(2k﹣1)x+k2+1=0有两个不相等的实数根x1,x2.
(1)求实数k的取值范围;
(2)若方程的两实数根x1,x2满足|x1|+|x2|=x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校选派一部分学生参加“六盘水市马拉松比赛”,要为每位参赛学生购买一顶帽子.商场规定:凡一次性购买200顶或200顶以上,可按批发价付款;购买200顶以下只能按零售价付款.如果为每位参赛学生购买1顶,那么只能按零售价付款,需用900元;如果多购买45顶,那么可以按批发价付款,同样需用900元.问:
(1)参赛学生人数x在什么范围内?
(2)若按批发价购买15顶与按零售价购买12顶的款相同,那么参赛学生人数x是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC和△CDE都是等腰直角三角形,∠ACB=∠DCE=90°,且点A在ED的延长线上,以DE为直径的⊙O与AB交于G、H两点,连接BE.
(1)求证:BE是⊙O的切线;
(2)如图②,连接OB、OC,若tan∠CAD=![]() ,试判断四边形BECO的形状,请说明理由;
,试判断四边形BECO的形状,请说明理由;
(3)在(2)的条件下,若BF=![]() ,请你求出HG的长.
,请你求出HG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
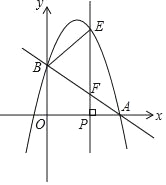
【题目】如图,在平面直角坐标系中,直线y=-![]() x+2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
x+2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
(1)点A的坐标为 .
(2)求这条抛物线所对应的函数表达式.
(3)点P在线段OA上时,若以B、E、F为顶点的三角形与△FPA相似,求m的值.
(4)若E、F、P三个点中恰有一点是其它两点所连线段的中点(三点重合除外),称E、F、P三点为“共谐点”.直接写出E、F、P三点成为“共谐点”时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的延长线上一点,且∠PDB=
的延长线上一点,且∠PDB=![]() ∠A,连接
∠A,连接![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)填空:
①当![]() 的度数为______时,四边形
的度数为______时,四边形![]() 是菱形;
是菱形;
②当![]() 时,
时,![]() 的面积为_________.
的面积为_________.
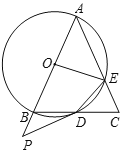
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com