
| AB |
| BC |
| CE |
| CG |
| DE |
| BG |
| AB |
| BC |
| EC |
| CG |
| DC |
| BC |
| EC |
| CG |
| DE |
| BG |
| 2 |
| 2 |
| 2 |
| 2 |


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 论.
论.查看答案和解析>>
科目:初中数学 来源:湖北省咸宁市2010年中考数学试卷 题型:059
问题背景
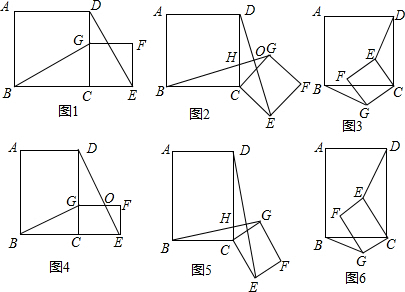
(1)如图,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:
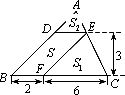
四边形DBFE的面积S=________,
△EFC的面积S1=________,
△ADE的面积S2=________.
探究发现
(2)在(1)中,若BF=a,FC=b,DE与BC间的距离为h.请证明S2=4S1S2.
拓展迁移
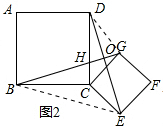
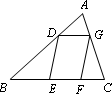
(3)如图,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源:2012届江苏省江阴市石庄中学九年级中考模拟考试数学试卷(带解析) 题型:解答题
问题背景:
如图1,矩形铁片ABCD的长为2a,宽为a; 为了要让铁片能穿过直径为 的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
探究发现:
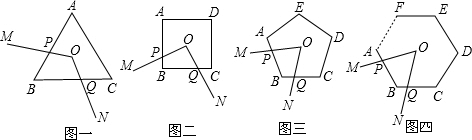
【小题1】如图2,M、N、P、Q分别是AD、AB、BC、CD的中点,若将矩形铁片的四个角去掉,只余下四边形MNPQ,则此时铁片的形状是 _______,给出证明,并通过计算说明此时铁片都能穿过圆孔;
拓展迁移:
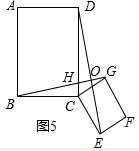
【小题2】如图3,过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合),沿着这条直线将矩形 铁片切割成两个全等的直角梯形铁片;
①当BE=DF= 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
②为了能使直角梯形铁片EBAF顺利穿过圆孔,请直接写出线段BE的长度的取值范围 .
查看答案和解析>>
科目:初中数学 来源:2013届江苏省赣榆县罗阳中学九年级4月质量检测(一)数学试卷(带解析) 题型:解答题
问题背景
(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:四边形DBFE的面积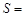 ,△EFC的面积
,△EFC的面积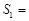 ,△ADE的面积
,△ADE的面积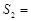 .
.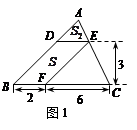
探究发现
(2)在(1)中,若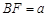 ,
, ,DE与BC间的距离为
,DE与BC间的距离为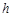 .请证明
.请证明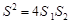 .
.
拓展迁移
(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积.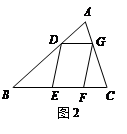
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com