
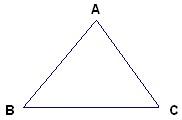
 27、已知△ABC,求证:∠A+∠B+∠C=180°.
27、已知△ABC,求证:∠A+∠B+∠C=180°.科目:初中数学 来源: 题型:
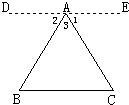 28、阅读下面的证明过程,指出其错误.
28、阅读下面的证明过程,指出其错误.查看答案和解析>>
科目:初中数学 来源: 题型:
 28、仅通过观察、试验等可以寻找规律,但是由于观察可能有误差,这样仅通过观察、试验等就下结论有时也缺乏说服力,所以得出的结论还需要证明.
28、仅通过观察、试验等可以寻找规律,但是由于观察可能有误差,这样仅通过观察、试验等就下结论有时也缺乏说服力,所以得出的结论还需要证明.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年四川省九年级上学期10月月考数学卷 题型:解答题
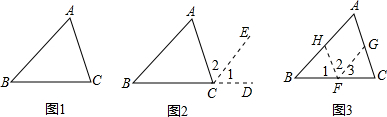
(12分)如图1,在⊿ABC中,AB=BC,P为AB边上一点,连接CP,以PA,PC为邻边作平行四边形APCD,AC与PD相交于点E,已知∠ABC=∠AEP=

1.①.求证:∠EAP=∠EPA;
2. ②.平行四边形APCD是否为矩形?请说明理由;
3.③.如图2,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M,N分别是∠MEN的两边与BA,FP延长线的交点),猜想线段EM与EN之间的数量关系,并证明你的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com