
分析 (1)约去分式中的分子与分母的公因式,即可得出答案.
(2)先将分子与分母进行因式分解,再根据分式的基本性质,将分子与分母的公因式约去,即可求解.
解答 解:(1)$\frac{{-15{a^2}{b^3}}}{{25{a^5}{b^4}}}$=-$\frac{3}{{5{a^3}b}}$;
(2)$\frac{{{x^2}-4}}{x+2}$=$\frac{(x+2)(x-2)}{x+2}$=x-2.
点评 此题考查了约分,约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.由约分的概念可知,要首先将分子、分母转化为乘积的形式,再找出分子、分母的最大公因式并约去,注意不要忽视数字系数的约分.


科目:初中数学 来源: 题型:解答题
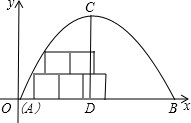 如图,某地下室横截面呈抛物线形,已知跨度AB=6m,最高点C到地面的距离CD=3m.
如图,某地下室横截面呈抛物线形,已知跨度AB=6m,最高点C到地面的距离CD=3m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com