
【题目】如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD. 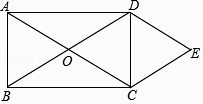
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的面积为10 ![]() ,求AC的长.
,求AC的长.
【答案】
(1)证明:∵CE∥BD,DE∥AC,
∴四边形OCED是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD,OA=OC,OB=OD,∠ADC=∠ABC=∠BAD=90°,
∴OD=OC,
∴四边形OCED是菱形
(2)解:∵四边形OCED是菱形,
∴菱形OCED的面积=2△OCD的面积=△ACD的面积= ![]() ADCD=10
ADCD=10 ![]() ,
,
∵∠ACB=30°,
∴∠BAC=60°,
∴∠DAC=30°,
∴AC=2CD,AD= ![]() CD,
CD,
∴ ![]() ×
× ![]() CDCD=10
CDCD=10 ![]() ,
,
解得:CD=2 ![]() ,
,
∴AC=2CD=4 ![]()
【解析】(1)首先由CE∥BD,DE∥AC,可证得四边形CODE是平行四边形,又由四边形ABCD是矩形,根据矩形的性质,易得OC=OD,即可判定四边形CODE是菱形,(2)根据菱形OCED的面积=2△OCD的面积=△ACD的面积= ![]() ADCD=10
ADCD=10 ![]() ,证出AC=2CD,AD=
,证出AC=2CD,AD= ![]() CD,得出
CD,得出 ![]() ×
× ![]() CDCD=10
CDCD=10 ![]() ,求出CD,即可得出答案.
,求出CD,即可得出答案.
【考点精析】通过灵活运用矩形的性质,掌握矩形的四个角都是直角,矩形的对角线相等即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图是甲、乙两公司近年销售收入情况的折线统计图,根据统计图得出下列结论,其中正确的是( )
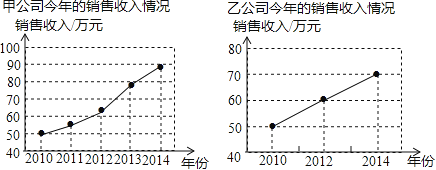
A.甲公司近年的销售收入增长速度比乙公司快
B.乙公司近年的销售收入增长速度比甲公司快
C.甲、乙两公司近年的销售收入增长速度一样快
D.不能确定甲、乙两公司近年销售收入增长速度的快慢
查看答案和解析>>
科目:初中数学 来源: 题型:
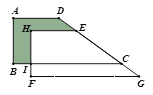
【题目】如图所示,直角梯形ABCD 沿直线DC方向平移可得直角梯形HFGE,如果AB=4,BC=9,BI=1.2,HI=3那么阴影面积为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名学生中选拨一人参加射击比赛,对他们的射击水平进行了测验,两人在相同条件下各射靶6次,命中的环数如下:
甲:7,8,6,10,10,7
乙:7, 7,8,8,10,8,
如果你是教练你会选拨谁参加比赛?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
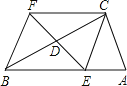
【题目】如图,在△ABC中,∠ACB=90°,且DE是△ABC的中位线.延长ED到F,使DF=ED,连接FC,FB.回答下列问题:
(1)试说明四边形BECF是菱形.
(2)当![]() 的大小满足什么条件时,菱形BECF是正方形?请回答并证明你的结论.
的大小满足什么条件时,菱形BECF是正方形?请回答并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0)两点,与y轴交于点C(0,3).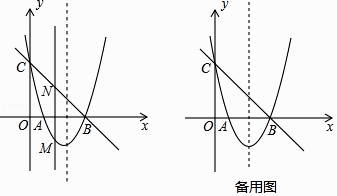
(1)求抛物线的解析式;
(2)若点M是x轴下方的抛物线上的一个动点,过点M作MN⊥x轴,交直线BC于点N,求四边形MBNA的最大面积,并求出点M的坐标;
(3)在抛物线上是否存在一点P,使△BCP为直角三角形?若存在,求出P点坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
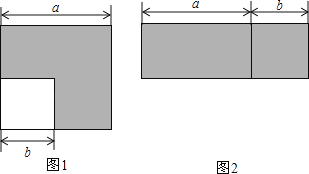
【题目】如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个正方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则 ![]() 的值为 .
的值为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com