
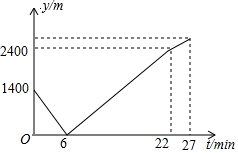
 小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①由当t=0时y=1400,可得出打电话时,小东和妈妈的距离为1400米,结论①正确;②利用速度=路程÷时间结合小东的速度,可求出小东和妈妈相遇后,妈妈回家的速度为50m/min,结论②正确;③由t的最大值为27,可得出小东打完电话后,经过27min到达学校,结论③正确;④根据路程=2400+小东步行的速度×(27-22),即可得出小东家离学校的距离为2900m,结论④正确.综上即可得出结论.
解答 解:①当t=0时,y=1400,
∴打电话时,小东和妈妈的距离为1400米,结论①正确;
②2400÷(22-6)-100=50(m/min),
∴小东和妈妈相遇后,妈妈回家的速度为50m/min,结论②正确;
③∵t的最大值为27,
∴小东打完电话后,经过27min到达学校,结论③正确;
④2400+(27-22)×100=2900(m),
∴小东家离学校的距离为2900m,结论④正确.
综上所述,正确的结论有:①②③④.
故选D.
点评 本题考查了一次函数的应用,观察图形,逐一分析四条结论的正误是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-$\frac{8}{x}$的图象有一交点为A(-2,b)点.
如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-$\frac{8}{x}$的图象有一交点为A(-2,b)点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
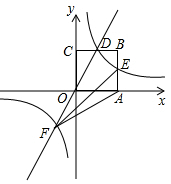 如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,点C分别在x轴,y轴的正半轴上,函数y=2x的图象与CB交于点D,函数y=$\frac{k}{x}$(k为常数,k≠0)的图象经过点D,与AB交于点E,与函数y=2x的图象在第三象限内交于点F,连接AF、EF.
如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,点C分别在x轴,y轴的正半轴上,函数y=2x的图象与CB交于点D,函数y=$\frac{k}{x}$(k为常数,k≠0)的图象经过点D,与AB交于点E,与函数y=2x的图象在第三象限内交于点F,连接AF、EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
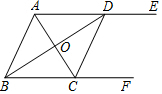 如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.
如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
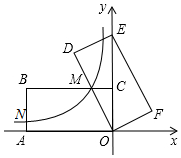 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=$\frac{k}{x}$(x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE=$\frac{1}{2}$,则BN的长为3.
如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=$\frac{k}{x}$(x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE=$\frac{1}{2}$,则BN的长为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
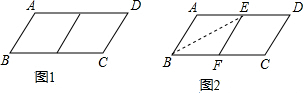 邻边不相等的平行四边形纸片,减去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,平行四边形ABCD中,若AB=1,BC=2,则平行四边形ABCD为1阶准菱形.
邻边不相等的平行四边形纸片,减去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,平行四边形ABCD中,若AB=1,BC=2,则平行四边形ABCD为1阶准菱形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com