
【题目】如图,AB是⊙O的直径,弦BC=4㎝,F是弦BC的中点,∠ABC=60°,若动点E以1 ㎝/s的速度从A点出发在AB上沿着A→B→A运动,设运动时间为t(s)(0≤t<16),连接EF,当△BEF是直角三角形时,t(s)的值为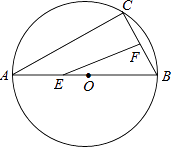
【答案】4.
【解析】根据圆周角定理得到∠C=90°,由于∠ABC=60°,BC=4cm,根据含30度的直角三角形三边的关系得到AB=2BC=8cm,而F是弦BC的中点,所以当EF∥AC时,△BEF是直角三角形,此时E为AB的中点,易得t=4s;当从A点出发运动到B点名,再运动到O点时,此时t=12s;也可以过F点作AB的垂线,点E点运动到垂足时,△BEF是直角三角形.
∵AB是⊙O的直径,
∴∠C=90°,
而∠ABC=60°,BC=4cm,
∴AB=2BC=8cm,
∵F是弦BC的中点,
∴当EF∥AC时,△BEF是直角三角形,
此时E为AB的中点,即AE=AO=4cm,
∴t= ![]() =4.
=4.
【考点精析】本题主要考查了圆周角定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某工厂准备翻建新的大门,厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的运输卡车的高度是3m,宽度是5.8m.现设计了两种方案.方案一:建成抛物线形状(如图1);方案二:建成圆弧形状(如图2).为确保工厂的卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.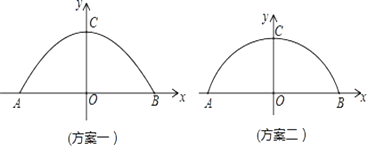
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分別在矩形ABCD的边AB、CD、DA上,AH=2.
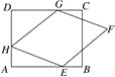
(1)已知DG=6,求AE的长;
(2)已知DG=2,求证:四边形EFGH为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B、E、C、F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明
如图,FG//CD,∠1=∠3,∠B=50°,求∠BDE的度数.
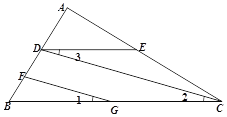
解:∵FG//CD (已知)
∴∠2=_________(____________________________)
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC//__________(_____________________________)
∴∠B+________=180°(______________________________)
又∵∠B=50°
∴∠BDE=________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
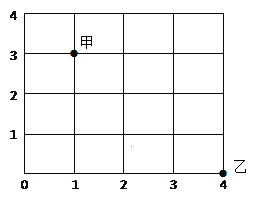
【题目】如图,甲处表示两条路的交叉口,乙处也是两条路的交叉口,如果用(1,3)表示甲处的位置,那么“(1,3)→(2,3)→(3,3)→(4,3)→(4,2)→(4,1)→(4,0)”表示甲处到乙处的一种路线,若图中一个单位长度表示5Km,请你用上述表示法写出甲处到乙处的另两种走法,最短距离是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是根据对初一(1)班的50名同学平时最爱吃的食物的种类进行的问卷调查绘制成的统计表,请填满缺少的项并回答后面的问题.
肉类 | 蔬菜类 | 瓜果类 | 水产类 | |
男生 | 22 | 1 | 2 | |
女生 | 4 | 5 | 3 | |
频率 | 64% | 14% | 12% |
(1)选择适当的统计图表示男生平时最爱吃的食物的种类情况;
(2)就给出的初一(1)班的同学平时最爱吃的食物的种类情况,请你结合自己的年龄特点简略谈谈自己的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=8,延长线段AB至C,使得BC=![]() AB,延长线段BA至D,使得AD=
AB,延长线段BA至D,使得AD=![]() AB,则下列判断正确的是 ( )
AB,则下列判断正确的是 ( )
A. BC=![]() AD B. BD=3BC C. BD=4AD D. AC=6AD
AD B. BD=3BC C. BD=4AD D. AC=6AD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com