
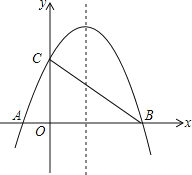
����Ŀ����ͼ����֪������y=��![]() +bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪B�������ΪB��8��0����
+bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪B�������ΪB��8��0����
��1���������ߵĽ���ʽ����Գ��᷽�̣�
��2������AC��BC�����жϡ�AOC���COB�Ƿ����ƣ���˵�����ɣ�
��3��MΪ��������BC֮���һ�㣬NΪ�߶�BC�ϵ�һ�㣬��MN��y�ᣬ��MN�����ֵ��
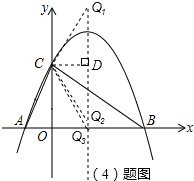
��4���������ߵĶԳ������Ƿ���ڵ�Q��ʹ��ACQΪ���������Σ������ڣ��������������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��![]() x2+
x2+![]() x+4��x=3����2����AOC�ס�COB�����ɼ���������3��4����4����Q������Ϊ��3��4+
x+4��x=3����2����AOC�ס�COB�����ɼ���������3��4����4����Q������Ϊ��3��4+![]() ����3��4��
����3��4��![]() ����3��0��
����3��0��
�������������������1���ѵ�B��������������߽���ʽ���b��ֵ�����ɵõ������߽���ʽ���ٸ��ݶԳ��᷽����ʽ���㼴�ɵý⣻
��2����y=0���ⷽ�������A�����꣬��x=0���y��ֵ�õ���C�����꣬�����OA��OB��OC��Ȼ����ݶ�Ӧ�߳ɱ������н���ȵ���������������֤����
��3����ֱ��BC�Ľ���ʽΪy=kx+b�����ô���ϵ�����������ʽ���ٱ�ʾ��MN��Ȼ����ݶ��κ�������ֵ������
��4�����ù��ɶ�����ʽ���AC������C��CD�ͶԳ�����D��Ȼ��֢�AC=CQʱ�����ù��ɶ�����ʽ���DQ���ֵ�Q�ڵ�D���Ϸ����·�������������Q��x��ľ��룬��д��������꼴�ɣ��ڵ�QΪ�Գ�����x��Ľ���ʱ��AQ=CQ����д����Q�����꼴�ɣ�
�����������1���ߵ�B��8��0����������y=��![]() +bx+4�ϣ�
+bx+4�ϣ�
����![]() ��64+8b+4=0��
��64+8b+4=0��
���b= ![]() ��
��
�������ߵĽ���ʽΪy=��![]() x2+
x2+![]() x+4��
x+4��
�Գ���Ϊֱ��x=��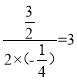
��2����AOC�ס�COB��
�������£���y=0����![]() x2+
x2+![]() x+4=0��
x+4=0��
��x2��6x��16=0��
���x1=��2��x2=8��
���A����������2��0����
��x=0����y=4��
���C��������0��4����
��OA=2��OB=8��OC=4��
��![]() ����AOC=��COB=90����
����AOC=��COB=90����
���AOC�ס�COB��
��3����ֱ��BC�Ľ���ʽΪy=kx+b��
��![]()
���![]()
��ֱ��BC�Ľ���ʽΪy=��![]() x+4��
x+4��
��MN��y�ᣬ
��MN=��![]() x2+
x2+![]() x+4������
x+4������![]() x+4����
x+4����
=��![]() x2+
x2+![]() x+4+
x+4+![]() x��4��
x��4��
=��![]() x2+2x��
x2+2x��
=��![]() ��x��4��2+4��
��x��4��2+4��
�൱x=4ʱ��MN��ֵ������ֵΪ4��
��4���ɹ��ɶ����ã�AC=![]() =2
=2![]() ��
��
����C��CD�ͶԳ�����D����CD=3��
��AC=CQʱ��DQ=![]() =
=![]() =
=![]() ��
��
��Q�ڵ�D���Ϸ�ʱ����Q��x��ľ���Ϊ4+![]() ��
��
��ʱ��Q1��3��4+![]() ����
����
��Q�ڵ�D���·�ʱ����Q��x��ľ���Ϊ4��![]() ��
��
��ʱ��Q2��3��4��![]() ����
����
�ڵ�QΪ�Գ�����x��Ľ���ʱ��AQ=5��
CQ=![]() =5��
=5��
��AQ=CQ��
��ʱ����Q3��3��0����
�۵�AC=AQʱ����AC=2![]() ����A���Գ���ľ���Ϊ5��2
����A���Գ���ľ���Ϊ5��2![]() ��5�����������β����ڣ�
��5�����������β����ڣ�
������������Q��������3��4+![]() ����3��4��
����3��4��![]() ����3��0��ʱ����ACQΪ����������ʱ��
����3��0��ʱ����ACQΪ����������ʱ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�У�y����x�ĺ������ǣ�������
A. y=|x| B. y=x C. y=��x+1 D. y=��x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ı���ABCD��ƽ���ı��Σ�DE��AC����BC���ӳ����ڵ�E��EF��AB�ڵ�F����֤��AD=CF��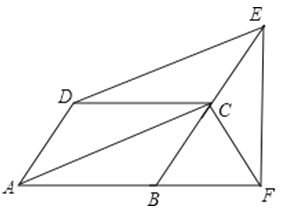
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʡ��S226�����ؾ���ij·��ʵ�����٣�����������ʻ�ٶȲ��ó���60km/h����ͼ��һ��С���������·��ֱ����ʻ��ijһʱ�̸պ���ʻ��·���泵�ټ����A������ǰ��36m��C��������3s���С�����복�ټ���Ǽ����Ϊ60m������С������������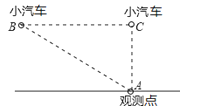
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷�������̼���У�2016��10��1�����ij��й������г�����ϵͳ��һ�ڣ������У�Խ��Խ��ľ���ѡ�����г���Ϊ���еĽ�ͨ���ߣ�����ij��ѧ������ȤС��Ϊ���˽�ijС��������з�ʽ�ı仯����������ȡ�˸�С�����־�����е��飬����������ͼ������ͳ��ͼ������ͳ��ͼ��������Ϣδ������

����������ͳ��ͼ������������⣺
��1����������������� ______ �ˣ�
��2���������г�����ϵͳ���к��������ѡ�����г���Ϊ���з�ʽ�İٷֱ�����˶��٣�
��3�������С�����о���2000�ˣ��������г�����ϵͳ���к����ѡ�����г���Ϊ���з�ʽ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼�Ϊ��Ȼ�¼����ǣ� ��
A.���ӻ�������Ƶ��������ɽ������̨
B.��һ���˿�����������һ���ƣ���ɫ�Ǻ���
C.��һ�ŵ�ӰƱ����λ������������
D.�ڴ���װ��4�������2������������3�������б��к���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��ԭ����������������˶���ͬʱ����BҲ��ԭ����������������˶���3s���������18����λ���ȣ���֪��B���ٶ��ǵ�A���ٶȵ�5��(�ٶȵ�λ����λ���ȣ�s)��
��1�������A����B�˶����ٶȣ����������ϱ��A��B�����ԭ������˶�3sʱ��λ�ã�
��2����A��B�����(1)�е�λ�ÿ�ʼ������ԭ�����ٶ�ͬʱ�����������˶�������ʱ��ԭ��ǡ�ô��ڵ�A����B�����м�?
��3����A��B�����(2)�е�λ�ü�����ԭ�����ٶ������������˶���ͬʱ����һ��C��ԭ��λ��Ҳ���A�˶�����������A�������������B�˶���������B���������������A�˶������������ֱ����B�ϵ�Aʱ����C����ֹͣ�˶�������Cһֱ��8����λ���ȣ�s���ٶ������˶������C�ӿ�ʼ�˶���ֹͣ�˶�����ʻ��·���Ƕ��ٸ���λ����?
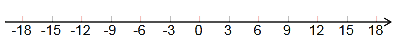
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com