
 ,cos30°=
,cos30°= ,tan30°=
,tan30°= .)
.)
 ,-
,- ).
). 解:(1)设旋转后点A落在抛物线上点A1处,OA1=OA=1,
解:(1)设旋转后点A落在抛物线上点A1处,OA1=OA=1,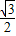 ,A1M=OA1sin30°=
,A1M=OA1sin30°= ,
, ,-
,- ).
). =a(
=a( )2
)2 ,
, x2
x2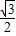 ,-
,- ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2005年全国中考数学试题汇编《一次函数》(06)(解析版) 题型:解答题
 x,AD=8.矩形ABCD沿DB方向以每秒1个单位长度运动,同时点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C,用了14秒.
x,AD=8.矩形ABCD沿DB方向以每秒1个单位长度运动,同时点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C,用了14秒.
查看答案和解析>>
科目:初中数学 来源:2005年吉林省长春市中考数学试卷(课标卷)(解析版) 题型:解答题
 x,AD=8.矩形ABCD沿DB方向以每秒1个单位长度运动,同时点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C,用了14秒.
x,AD=8.矩形ABCD沿DB方向以每秒1个单位长度运动,同时点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C,用了14秒.
查看答案和解析>>
科目:初中数学 来源:2005年吉林省长春市中考数学试卷(课标卷)(解析版) 题型:解答题
 ,cos30°=
,cos30°=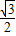 ,tan30°=
,tan30°= .)
.)
查看答案和解析>>
科目:初中数学 来源:2005年吉林省长春市中考数学试卷(课标卷)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com