
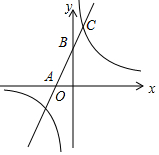
 如图,在平面直角坐标系xOy中,直线y=2x+2与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$(k≠0)的一个交点为点C(1,m).
如图,在平面直角坐标系xOy中,直线y=2x+2与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$(k≠0)的一个交点为点C(1,m).分析 (1)根据坐标与图形的关系求出m,利用待定系数法计算即可;
(2)分AB∥DP和PB∥DA两种情况,根据平行四边形的判定定理解答即可.
解答 解:(1)∵点C(1,m)在直线y=2x+2上,
∴m=4,
∵点C(1,4)在双曲线$y=\frac{k}{x}$上,
∴k=4.
∴双曲线的表达式为$y=\frac{4}{x}$;
(2)当x=0时,y=2x+2=0,
∴点B的坐标为(0,2),
∵BD∥x轴,
∴点D的横坐标为2,
∴点D的坐标是(2,2),
当y=2时,2x+2=0,
解得,x=-1,
则当A的坐标为(-1,0),
∴当AB∥DP时,点P的坐标为(1,0),
当PB∥DA时,点P的坐标为(-3,0),
∴点P的坐标为(1,0)或(-3,0)时,以点A,B,D,P为顶点的四边形为平行四边形.
点评 本题考查的是一次函数与反比例函数的交点问题、平行四边形的判定,掌握待定系数法求函数解析式、灵活运用分情况讨论思想是解题的关键.


科目:初中数学 来源: 题型:填空题
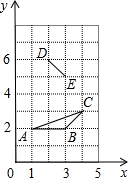 如图,已知A,B,C,D,E五点的坐标分别为(1,2),(3,2),(4,3),(2,6),(3,5).如果点F在第-象限内,且以D,E,F为顶点的三角形与△ABC全等,那么点F的坐标为(2,8)或(0,6)或(5,5)或(3,3).
如图,已知A,B,C,D,E五点的坐标分别为(1,2),(3,2),(4,3),(2,6),(3,5).如果点F在第-象限内,且以D,E,F为顶点的三角形与△ABC全等,那么点F的坐标为(2,8)或(0,6)或(5,5)或(3,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
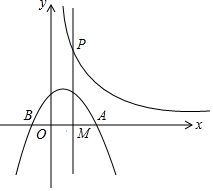 如图,抛物线C:y=-$\frac{1}{2}$(x-t)(x-t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,若OA•MP=12.
如图,抛物线C:y=-$\frac{1}{2}$(x-t)(x-t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,若OA•MP=12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 0.9 | B. | 1.0 | C. | 1.1 | D. | 1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在数学活动课上,老师带领学生去测量操场上树立的旗杆的高度,老师为同学们准备了如下工具:①高为m米的测角仪,②长为n米的竹竿,③足够长的皮尺.请你选用以上的工具,设计一个可以通过测量,求出国旗杆高度的方案(不用计算和说明,画出图形并标记可以测量的长度或者角度即可,可测量的角度选用α,β,γ标记,可测量的长度选用a,b,c,d标记,测角仪和竹竿可以用线段表示).
在数学活动课上,老师带领学生去测量操场上树立的旗杆的高度,老师为同学们准备了如下工具:①高为m米的测角仪,②长为n米的竹竿,③足够长的皮尺.请你选用以上的工具,设计一个可以通过测量,求出国旗杆高度的方案(不用计算和说明,画出图形并标记可以测量的长度或者角度即可,可测量的角度选用α,β,γ标记,可测量的长度选用a,b,c,d标记,测角仪和竹竿可以用线段表示).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12%+7%=x% | B. | (1+12%)(1+7%)=2(1+x%) | C. | 12%+7%=2x% | D. | (1+12%)(1+7%)=(1+x%)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com