
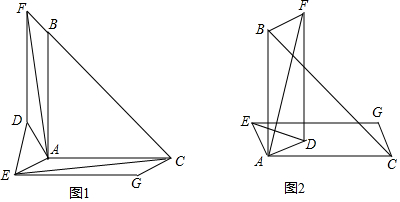
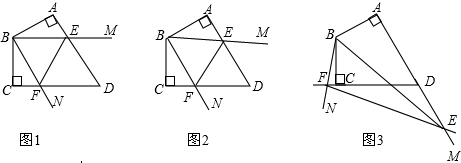
分析 (1)如图1,先利用SAS证明△EAC≌△FBA,则EC=AF,∠AFB=∠AEC,再延长FA交EC于G,证∠AEC+∠EAG=90°,即可得AF⊥EC;
(2)如图2,结论仍然成立,同理可证△EAC≌△FBA,则EC=AF,∠BAF=∠ECA,再由直角△ANC中两锐角互余得出结论.
解答 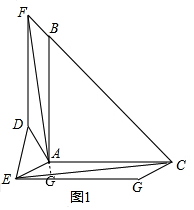 证明:(1)如图1,∵△ABC与△ADE都是等腰直角三角形,
证明:(1)如图1,∵△ABC与△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,
∵四边形ABFD是平行四边形,
∴AD=BF,AD∥BF,
∴BF=AE,
∵AD∥BF,
∴∠DAB+∠FBA=180°,
∵∠DAE=∠BAC=90°,
∴∠DAB+∠EAC=180°,
∴∠EAC=∠FBA,
在△EAC和△FBA中,
∵$\left\{\begin{array}{l}{AE=BF}\\{∠EAC=∠FBA}\\{AC=AB}\end{array}\right.$,
∴△EAC≌△FBA(SAS),
∴EC=AF,∠AFB=∠AEC,
延长FA交EC于G,
∵AD∥FB,
∴∠AFB=∠DAF,
∴∠DAF=∠AEC,
∵∠DAE=90°,
∴∠DAF+∠EAG=90°,
∴∠AEC+∠EAG=90°,
∴∠AGE=90°,
∴AF⊥BC;
(2)如图2,结论仍然成立,理由是: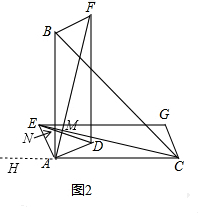
同理得:AB=AC,BF=AE,
作射线CA至H,则∠HAE+∠EAC=180°,
∵BF∥AD,
∴∠FBA+∠BAD=180°,
∵∠BAH=∠EAD=90°,
∴∠HAE+∠EAB=90°,∠BAD+∠EAB=90°,
∴∠HAE=∠BAD,
∴∠EAC=∠FBA,
∴△EAC≌△FBA,
∴AF=EC,∠BAF=∠ECA,
设CE与AB交于N,AF与EC交于点M,
∵∠BAC=90°,
∴∠ECA+∠ANC=90°,
∴∠BAF+∠ANC=90°,
∴∠AME=90°,
∴AF⊥EC.
点评 本题考查了等腰直角三角形、平行四边形、全等三角形的性质和判定,此类题型是常考题型,以证明三角形全等这突破口,两问的证法类似,但本题的图形较为复杂,所以要认真观察,利用平行四边形边和角的性质得出有利于三角形全等的条件,从而使问题得以解决.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 10,24,26 | B. | 15,20,25 | C. | 8,10,12 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
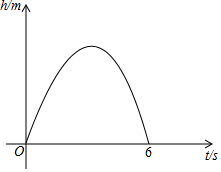 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
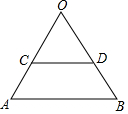 如图,△ABO是正三角形,CD∥AB,把△ABO绕△OCD的内心P旋转180°得到△EFG
如图,△ABO是正三角形,CD∥AB,把△ABO绕△OCD的内心P旋转180°得到△EFG查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com