
【题目】已知:如图,∠D=110°,∠EFD=70°,∠1=∠2,求证:∠3=∠B
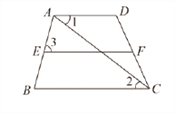
证明:
∵∠D=110°,∠EFD=70°(已知)
∴∠D+∠EFD=180°
∴AD∥EF( )
又∵∠1=∠2(已知)
∴ ∥ (内错角相等,两直线平行)
∴EF∥BC( )
∴∠3=∠B( )
科目:初中数学 来源: 题型:
【题目】如图,在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶.在航行到B处时,发现灯塔A在我军舰的正北方向500米处;当该军舰从B处向正西方向行驶至达C处时,发现灯塔A在我军舰的北偏东60°的方向.求该军舰行驶的路程.(计算过程和结果均不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知n(n≥3,且n为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当n=3时,共有2个交点;当n=4时,共有5个交点;当n=5时,共有9个交点;…依此规律,当共有交点个数为27时,则n的值为( )
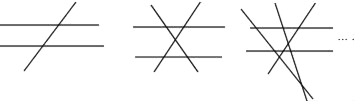
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折叠三角形纸片ABC,使点A落在BC边上的点F,且折痕DE∥BC,若∠A=75°,∠C=60°,则∠BDF=____________________________
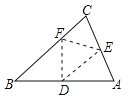
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,E是BC边的中点,连接AE,F为CD边上一点,且满足∠DFA=2∠BAE.

(1)若∠D=105°,∠DAF=35°.求∠FAE的度数;
(2)求证:AF=CD+CF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com