
【题目】如图,已知在等腰 Rt△ABC中,∠C=90°,斜边AB=2,若将△ABC翻折,折痕EF分别交边AC、边BC于点E和点F(点E不与A点重合,点F不与B点重合),且点C落在AB边上,记作点D.过点D作DK⊥AB,交射线AC于点K,设AD=x,y=cot∠CFE,
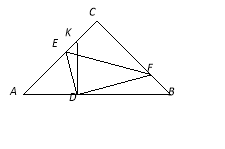

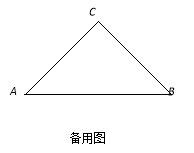
(1)求证:△DEK∽△DFB;
(2)求y关于x的函数解析式并写出定义域;
(3)联结CD,当![]() =
=![]() 时,求x的值.
时,求x的值.
【答案】(1)证明见解析(2)y=![]() ,定义域:2-
,定义域:2-![]() <x<
<x<![]() (3)x=
(3)x=![]() -1或3-
-1或3-![]() .
.
【解析】
试题分析:(1)利用等腰直角三角形的性质证明∠EKD=∠B,利用图形折叠的性质得到∠EDK=∠FDB,即可得出结论;(2)利用△DEK∽△DFB,得出![]() =
=![]() ,从而y=cot∠CFE=cot∠DFE=
,从而y=cot∠CFE=cot∠DFE=![]() =
=![]()
![]() 代入化简即可,定义域:2-
代入化简即可,定义域:2-![]() <x<
<x<![]() (3)取线段EF的中点O,连接OC、OD,根据直角三角形斜边上的中线等于斜边的一半可得OC=OD=
(3)取线段EF的中点O,连接OC、OD,根据直角三角形斜边上的中线等于斜边的一半可得OC=OD=![]() EF.设EF与CD交点为H,根据轴对称的性质可得EF⊥CD,且CH=DH=
EF.设EF与CD交点为H,根据轴对称的性质可得EF⊥CD,且CH=DH=![]() CD.由
CD.由![]() 可得tan∠HOC=
可得tan∠HOC=![]() ,从而得到∠HOC=60°,然后分①若点K在线段AC上和②若点K在线段AC的延长线上,两种情况讨论,得到y的值,再把y的值代入函数解析式就可求出x的值.
,从而得到∠HOC=60°,然后分①若点K在线段AC上和②若点K在线段AC的延长线上,两种情况讨论,得到y的值,再把y的值代入函数解析式就可求出x的值.
试题解析:(1)在等腰 Rt△ABC中,∠C=90°,∴∠A=∠B=45°
又∵DK⊥AB,∴∠EKD=45°∴∠EKD=∠B
∵将△ABC翻折后点C落在AB边上的点D处
∴∠EDF=∠C=90°
∵∠KDA= ∠KDB=90°
∴∠EDK=90°-∠KDF, ∠FDB=90°-∠KDF
∴∠EDK=∠FDB
∴△DEK∽△DFB
(说明:点K在线段AC延长线上时等同于在线段上的相似的情况,故不必分类证明)
(2)∵△DEK∽△DFB,∴![]() =
=![]()
∵∠DFE=∠CFE,∴y=cot∠CFE=cot∠DFE=![]() =
=![]()
∵AD=x,AB=2,∴DK=AD=x,DB=2-x,∴![]() =
=![]() ,∴y=
,∴y=![]()
![]() 定义域:2-
定义域:2-![]() <x<
<x<![]()
(3)方法一:设CD与EF交于点H,CD被折痕EF垂直平分,CD=2 CH
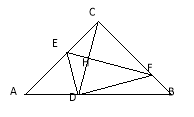
∵![]() =
=![]() ,∴
,∴![]() =
=![]() ,设CH=
,设CH=![]() ,EF=4
,EF=4![]()
∵CD⊥EF,∠C=90°
∴∠EHC=∠CHF=90°, ∠ECH=∠CFH=90°-∠HCF
![]() ∴△ECH∽△CFH, 得:∴
∴△ECH∽△CFH, 得:∴![]() =
=![]() , 即
, 即![]()
设EH=a,则得:![]()
![]() 解得:
解得:![]()
当EH=k时,∠ECHspan>=∠CFE=30°,
∴y=![]() =cot30°=
=cot30°=![]() ,∴x=
,∴x=![]() -1;
-1;
当EH=3k时,∠ECH=∠CFE=60°,
∴y=![]() =cot60°=
=cot60°=![]() ,∴x=3-
,∴x=3-![]() ;
;
经检验:x=![]() -1,x=3-
-1,x=3-![]() 分别是原各方程的根,且符合题意;
分别是原各方程的根,且符合题意;
综上所述,x=![]() -1或x=3-
-1或x=3-![]() .
.
方法二:设CD与EF交于点H,取EF的中点O,联结OC,

∴CH⊥EF,CH=![]() CD,CO=
CD,CO=![]() EF.
EF.
∵![]() =
=![]() ,∴
,∴![]() =
=![]() .
.
当0<AD<1时(如图备一),在Rt△COH中,∠COH=60°,
∴∠CFE=30°,∴y=![]() =cot30°=
=cot30°=![]() ,∴x=
,∴x=![]() -1;
-1;
当1<AD<2时(如图备二),
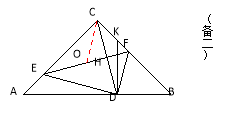
在Rt△COH中,∠COH=60°,
∴∠CFE=60°,∴y=![]() =cot60°=
=cot60°=![]() ,∴x=3-
,∴x=3-![]() .
.
经检验:x=![]() -1,x=3-
-1,x=3-![]() 分别是原各方程的根,且符合题意;
分别是原各方程的根,且符合题意;
综上所述,x=![]() -1或x=3-
-1或x=3-![]() .
.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(1,0)、B(4,0)、C(3,3)、D(1,4).
(1)描出A、B、C、D四点的位置,并顺次连结ABCD.
(2)四边形ABCD的面积是 .
(3)把四边形ABCD向左平移5个单位,再向上平移1个单位得到四边形A′B′C′D′,在图在画出四边形A′B′C′D′,并写出点A′、B′、C′、D′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价.在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
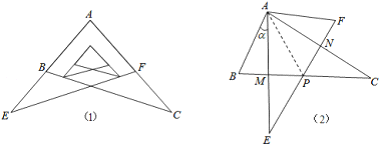
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD 中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.

(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像经过点A(0,4)和B(1,-2).
的图像经过点A(0,4)和B(1,-2).
(1)求此函数的解析式;并运用配方法,将此抛物线解析式化为y=a(x+m)2+k的形式;
(2)写出该抛物线顶点C的坐标,并求出△CAO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BO、CO分别是∠ABC、∠ACB的角平分线,求:

(1)若∠A=50°,求∠BOC的度数.
(2)在其他条件不变的情况下,若∠A=n°,则∠A与∠BOC之间有怎样的数量关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com