练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．如图，AB∥CD，AD与BC相交于点O，若AO=2，DO=4，BO=3，则BC的长为（　　）
    A．6B．9C．12D．15

    分析 由平行线分线段成比例定理，得到$\frac{BO}{CO}$=$\frac{AO}{DO}$；利用AO、BO、DO的长度，求出CO的长度，再根据BC=BO+CO即可解决问题．

    解答 解：∵AB∥CD，
    ∴$\frac{BO}{CO}$=$\frac{AO}{DO}$；
    ∵AO=2，DO=4，BO=3，
    ∴$\frac{3}{CO}$=$\frac{2}{4}$，解得：CO=6，
    ∴BC=BO+CO=3+6=9．
    故选B．

    点评 该题主要考查了平行线分线段成比例定理及其应用问题．掌握平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    20．下列手机屏幕解锁图案中，不是轴对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知：A、B、C三点共线，且线段AB=17cm，点D为BC的中点，AD=11cm，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．$\frac{3}{5}$的倒数是（　　）
    A．$\frac{3}{5}$B．-$\frac{3}{5}$C．$\frac{5}{3}$D．-$\frac{5}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，在平面直角坐标系中，抛物线y=ax2-2ax-3a（a＞0）与x轴交于A、B两点（点A在点B左侧），经过点A的直线l：y=kx+b与y轴交于点C，与抛物线的另一个交点为D，且CD=4AC．
    （1）直接写出点A的坐标，并用含a的式子表示直线l的函数表达式（其中k、b用含a的式子表示）．
    （2）点E为直线l下方抛物线上一点，当△ADE的面积的最大值为$\frac{25}{4}$时，求抛物线的函数表达式；
    （3）设点P是抛物线对称轴上的一点，点Q在抛物线上，以点A、D、P、Q为顶点的四边形能否为矩形？若能，求出点P的坐标；若不能，请说明理由．

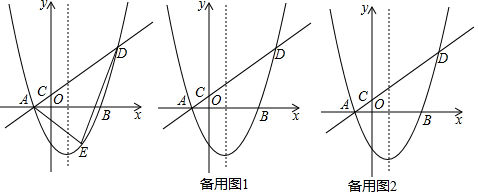
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，下列条件中能判断直线l1∥l2的是（　　）
    A．∠1=∠2B．∠1=∠5C．∠3=∠5D．∠1+∠3=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

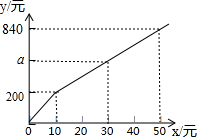    2．随着“中国诗词大会”节目的热播，《唐诗宋词精选》一书也随之热销．如果一次性购买10本以上，超过10本的那部分书的价格将打折，并依此得到付款金额y（单位：元）与一次性购买该书的数量x（单位：本）之间的函数关系如图所示，则下列结论错误的是（　　）
    A．一次性购买数量不超过10本时，销售价格为20元/本
    B．a=520
    C．一次性购买10本以上时，超过10本的那部分书的价格打八折
    D．一次性购买20本比分两次购买且每次购买10本少花80元

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

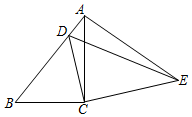    19．如图，在△ABC中，∠ACB=90°，AB=18，cosB=$\frac{2}{3}$，把△ABC绕着点C旋转，使点B与AB边上的点D重合，点A落在点E处，则线段AE的长为（　　）
    A．6$\sqrt{5}$B．7$\sqrt{5}$C．8$\sqrt{5}$D．9$\sqrt{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．菱形具有而平行四边形不具有的性质是（　　）
    A．对角线互相垂直B．两组对角分别相等
    C．对角线互相平分D．两组对边分别平行

    查看答案和解析>>

    同步练习册答案