
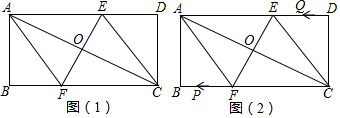
 如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,则∠AEO=30度.
如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,则∠AEO=30度. 分析 根据矩形的性质可得:OB=OC,AD∥BC,∠ABC=∠BAD=90°,又由AE平分∠BAD,∠AOD=120°,即可求得:∠OBE与∠AEB的度数,以及△OAB是等边三角形,△ABE是等腰三角形,即可得:△OBE是等腰三角形,求得∠OEB的度数,则问题得解.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=∠BAD=90°,AC=BD,OB=$\frac{1}{2}$BD,OC=$\frac{1}{2}$AC,
∴OB=OC,
∴∠OBC=∠OCB,
∵∠BOC=∠AOD=120°,
∴∠OBC=30°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=45°,
∴∠AEB=∠EAD=∠BAE=45°,
∴AB=BE,
∵∠AOD=120°,
∴∠AOB=60°,
∴AB=OA=OB,
∴OB=BE,
∴∠BOE=∠BEO,
∴∠OEB=75°,
∴∠AEO=∠OEB-∠AEB=75°-45°=30°.
故答案为:30.
点评 此题考查了矩形的性质.注意由平行线与角平分线则可构造等腰三角形,还要注意数形结合思想的应用.


科目:初中数学 来源: 题型:选择题
| A. | 4cm2 | B. | 6cm2 | C. | 8cm2 | D. | 12cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 对角线互相垂直平分的四边形是正方形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相平分的四边形是平行四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-5)^{2}}$=-5 | B. | $\sqrt{3}$×$\sqrt{4}$=$\sqrt{7}$ | C. | $\sqrt{12}$÷$\sqrt{3}$=2 | D. | (-$\sqrt{3}$)2=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=-$\frac{1}{2}$x+m(m>0)的图象与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.
如图,一次函数y=-$\frac{1}{2}$x+m(m>0)的图象与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一枚普通正六面体骰子所得点数不超过6 | |
| B. | 买一张体育彩票中一等奖 | |
| C. | 从实数-$\frac{2}{7},\sqrt{3},\root{3}{-8},\frac{1}{3}$π,0.1010010001中随机抽取一个数恰好是有理数 | |
| D. | 口袋中装有10 个红球,从中摸出一个是白球 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com