
已知:抛物线y=x2+bx+c与x轴交于P,Q两点,与y轴交于点E,且OE=OP=PQ.(1)画出抛物线的示意图,并求出抛物线的解析式;(2)问线段EQ上是否存在一点M,使△EMP∽△EPQ?若存在,求出点M的坐标;若不存在,请说明理由.
|
思路点拨:(1)抛物线开口向上,与x轴的两交点P、Q位居y轴的同侧,有两种情况,且P是线段OQ的中点; 由线段相等关系可得方程x2+bx+c=0两根,再用韦达定理列出方程组,并解之得抛物线解析式; (2)假设存在,由相似三角形对应边成比例,列出等式关系,求解得结论. 评注:本题主要考查了抛物线、一元二次方程、直线和相似三角形等知识,同时还考查了方程思想、数形结合思想、分类讨论思想.而第(2)小题又考查了一个存在性探索问题.因此本题思维层次高、运算量大、综合性强,要求考生具有较高的分析问题、探索问题和解决问题的能力. 一般情况下,解决条件探索题时,应先假设结论存在,并在此基础上,结合题设条件进行推理、计算,推出使结论成立的条件或说明不存在使结论成立的条件.由于此类问题的结构都比较复杂,所以往往需要分类讨论. 另外,本题中的两点P、Q会分居原点的两侧吗?事实上是不可能的.若P、Q两点分居原点两侧,则显然有OP<PQ,这与题设OP=PQ矛盾.故P、Q两点只能位于原点的同侧. |


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源:中考备考专家数学(第二版) 题型:044
已知:抛物线y=x2-mx+![]() 与抛物线y=x2+mx-
与抛物线y=x2+mx-![]() m2在平面直角坐标系xOy中的位置如图所示,其中一条与x轴交于A、B两点.
m2在平面直角坐标系xOy中的位置如图所示,其中一条与x轴交于A、B两点.
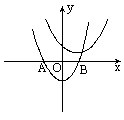
(1)试判断哪条抛物线经过A、B两点,并说明理由;
(2)若A、B两点到原点的距离AO、BO满足![]() -
-![]() =
=![]() ,求经过A、B两点的这条抛物线的解析式.
,求经过A、B两点的这条抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源:中考备考专家数学(第二版) 题型:044
已知:抛物线y=x2-(2m+4)x+m2-10与x轴交于A、B两点,C是抛物线的顶点.
(1)用配方法求顶点C的坐标(用含m的代数式表示);
(2)“若AB的长为2![]() ,求抛物线的解析式.”解法的部分步骤如下,补全解题过程,并简述步骤①的解题依据,步骤②的解题方法.
,求抛物线的解析式.”解法的部分步骤如下,补全解题过程,并简述步骤①的解题依据,步骤②的解题方法.
解:由(1)知,对称轴与x轴交于点D( ,0).
∵抛物线的对称性及AB=2![]() ,
,
∴AD=BD=|xA-xD|=![]() .
.
∵点A(xA,0)在抛物线y=(x-h)2+k上,
∴0=(xA-h)2+k. ①
∵h=xC=xD,将|xA-xD|=![]() 代入上式,得到关于m的方程
代入上式,得到关于m的方程
0=(![]() )2+( ) ②
)2+( ) ②
(3)将(2)中的条件“AB的长为2![]() ”改为“△ABC为等边三角形”,用类似的方法求出此抛物线的解析式.
”改为“△ABC为等边三角形”,用类似的方法求出此抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源:1+1轻巧夺冠优化训练九年级数学上 北京课改版 题型:044
已知:抛物线y=x2-(3m-1)x+m2-m.
(1)求证:此抛物线与x轴必有两个交点;
(2)若此抛物线与直线y=x-3m+3的一个交点在y轴上,求m的值.
查看答案和解析>>
科目:初中数学 来源:北京市延庆县2008年初中升学模拟试卷及答案、数学 题型:044
已知:抛物线y=x2+mx+n与x轴交A、B两点(A点在B点左侧),B(3,0),
且经过C(2,-3),与y轴交于点D,
(1)求此抛物线的解析式及顶点F的坐标;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物于E点,求线段PE长度的最大值;
(3)在(1)的条件下,在x轴上是否存在两个点G、H(G在H的左侧),且GH=2,使得线段GF+FC+CH+HG的长度和为最小;如果存在,求出G、H的坐标;如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com