
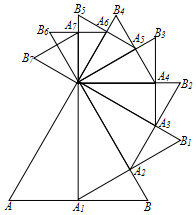
 已知等边△OAB的边长为a,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2;再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,△OAnBn,(如图),则△OA6B6的周长是$\frac{81}{64}$a..
已知等边△OAB的边长为a,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2;再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,△OAnBn,(如图),则△OA6B6的周长是$\frac{81}{64}$a.. 分析 在等边三角形中,由勾股定理可求得其一边上的高与边长的关系,根据图形的变化规律即可求解.
解答 解:依题意,OA1=$\frac{\sqrt{3}}{2}$OA、OA2=$\frac{\sqrt{3}}{2}$OA1=($\frac{\sqrt{3}}{2}$)2OA
OA3=$\frac{\sqrt{3}}{2}$OA2=($\frac{\sqrt{3}}{2}$)3OA
以此类推,OA6=($\frac{\sqrt{3}}{2}$)6OA=$\frac{27}{64}$OA=$\frac{27}{64}$a
即△OA6B6的周长=3OA6=$\frac{81}{64}$a.
故答案为:$\frac{81}{64}$a.
点评 本题是找规律题,找到第n个等边三角形的边长与前一个等边三角形的边长的关系是解题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
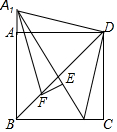 如图,在正方形ABCD中,点C1在边BC上,将△C1CD绕点D顺时针旋转90°得到△A1AD.A1F平分∠BA1C1,交BD于点F,过点F作FE⊥A1C1,垂足为E,当A1E=3,C1E=2时,则BD的长为$\frac{7\sqrt{2}}{2}$.
如图,在正方形ABCD中,点C1在边BC上,将△C1CD绕点D顺时针旋转90°得到△A1AD.A1F平分∠BA1C1,交BD于点F,过点F作FE⊥A1C1,垂足为E,当A1E=3,C1E=2时,则BD的长为$\frac{7\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
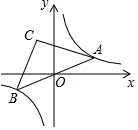 如图,点A是双曲线y=$\frac{6}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为y=-$\frac{6}{x}$.
如图,点A是双曲线y=$\frac{6}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为y=-$\frac{6}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.
如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com