
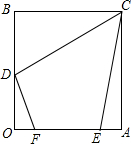
 如图,矩形OACB中,OA=3,OB=4,D为OB中点,E,F为OA上两动点,且EF=2,则四边形CDEF周长最小值为$\sqrt{13}$+$\sqrt{37}$+2.
如图,矩形OACB中,OA=3,OB=4,D为OB中点,E,F为OA上两动点,且EF=2,则四边形CDEF周长最小值为$\sqrt{13}$+$\sqrt{37}$+2. 分析 由于四边形CDEF中,CD、EF的长度为定值,欲求四边形CDEF周长的最小值,即求出DF和CE之和的最小值即可,为此,作点D关于OA的对称点M,作MN∥OA,使MN=2,连接CN,交OA于点E,过M点作MF∥EN,交OA于F,则此时四边形CDEF周长最小.
解答 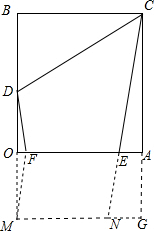 解:作点D关于OA的对称点M,作MN∥OA,使MN=2,连接CN,交OA于点E,过M点作MF∥EN,交OA于F,则此时四边形CDEF周长最小;
解:作点D关于OA的对称点M,作MN∥OA,使MN=2,连接CN,交OA于点E,过M点作MF∥EN,交OA于F,则此时四边形CDEF周长最小;
∵BC=3,BD=2,
∴CD=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
∵DF=MF=EN,
∴DF+CE=CN,
∵CN=$\sqrt{G{C}^{2}+G{N}^{2}}$=$\sqrt{(4+2)^{2}+(3-2)^{2}}$=$\sqrt{37}$,
∴四边形CDEF周长最小值为CD+EF+CN=$\sqrt{13}$+$\sqrt{37}$+2.
故答案为$\sqrt{13}$+$\sqrt{37}$+2.
点评 本题考查了轴对称-最短路线问题,矩形的性质,难度中等,求线段的和最小的问题基本的解题思路是根据轴对称转化为两点之间的距离的问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
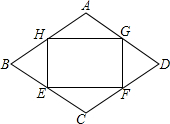 如图,菱形ABCD中,∠B=60°,AB=4cm,E、F、G、H分别是菱形四边中点,则四边形EFGH的面积为4$\sqrt{3}$cm2.
如图,菱形ABCD中,∠B=60°,AB=4cm,E、F、G、H分别是菱形四边中点,则四边形EFGH的面积为4$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
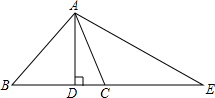 如图所示,AD是△ABC的高,延长BC至E,使CE=BC,△ABC的面积为S1,△ABE的面积为S2,那么S1=$\frac{1}{2}$S2.
如图所示,AD是△ABC的高,延长BC至E,使CE=BC,△ABC的面积为S1,△ABE的面积为S2,那么S1=$\frac{1}{2}$S2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小明和小亮相约晨练跑步,小明比小亮早1分钟离开家门,3分钟后迎面遇到从家跑来的小亮,两人沿滨江路跑了2分钟后,决定进行长跑比赛,比赛时小明的速度始终是180米/分,小亮的速度始终是220米/分.如图是两人之间的距离y(米)与小明离开家的时间x(分)之间的函数图象,下列说法:
小明和小亮相约晨练跑步,小明比小亮早1分钟离开家门,3分钟后迎面遇到从家跑来的小亮,两人沿滨江路跑了2分钟后,决定进行长跑比赛,比赛时小明的速度始终是180米/分,小亮的速度始终是220米/分.如图是两人之间的距离y(米)与小明离开家的时间x(分)之间的函数图象,下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com