Question

顺次连接四边形各边中点，所得的图形是________．顺次连接对角线________的四边形的各边中点所得的图形是矩形．顺次连接对角线________的四边形的各边中点所得的四边形是菱形．顺次连接对角线________的四边形的各边中点所得的四边形是正方形．

Answer 1

平行四边形    互相垂直    相等    互相垂直且相等
分析：新四边形的一组对边平行且等于一条对角线的一半，那么为平行四边形；新四边形的各边都等于相等的对角线的一半，所以为菱形；新四边形的各边都与原四边形的对角线垂直，那么各角均为90°，所以为矩形；矩形和菱形的结合为正方形．
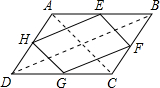
解答：解：顺次连接四边形各边中点，所得的图形是平行四边形；
（如图）根据中位线定理可得：GF=BD且GF∥BD，EH=BD且EH∥BD
∴EH=FG，EH∥FG
∴四边形EFGH是平行四边形；
顺次连接对角线互相垂直的四边形的各边中点所得的图形是矩形；
如图：
∵E、F、G、H分别为各边中点
∴EF∥GH∥DB，EF=GH=DB
EH=FG=AC，EH∥FG∥AC
∵DB⊥AC
∴EF⊥EH
∴四边形EFGH是矩形；
顺次连接对角线相等的四边形的各边中点所得的四边形是菱形；
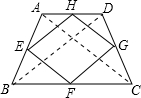
如图，
∵AC=BD，E、F、G、H分别是线段AB、BC、CD、AD的中点
∴EH、FG分别是△ABD、△BCD的中位线，EF、HG分别是△ACD、△ABC的中位线
根据三角形的中位线的性质
∴EH=FG=BD，EF=HG=AC
∵AC=BD
∴EH=FG=FG=EF
∴四边形EFGH是菱形；
根据正方形的判别方法知，对角线互相平分，互相垂直且相等的四边形是正方形．
故答案为平行四边形、互相垂直、相等、互相垂直且相等．
点评：本题考查的是正方形的判定、三角形中位线定理、平行四边形的判定、菱形的判定和矩形的判定．三角形的中位线平行于底边且等于底边的一半．解答此题的关键是根据题意画出图形，利用数形结合解答．