
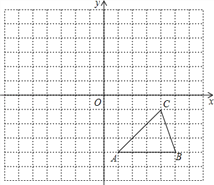
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1,并写出A1、B1、C1的坐标.
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】某学校计划组织师生参加哈尔滨冰雪节,感受冰雪艺术的魅力.出租公司现有甲、乙两种型号的客车可供租用,且每辆乙型客车的租金比每辆甲型客车少60元.若该校租用3辆甲种客车,4辆乙种客车,则需付租金1720元.
(1)该出租公司每辆甲、乙两型客车的租金各为多少元?
(2)若学校计划租用6辆客车,租车的总租金不超过1560元,那么最多租用甲型客车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,在四边形ABCD中,AD∥BC,点E在BC的延长线上,CE=BC,连接AE,交CD边于点F,且CF=DF.(1)求证:AD=BC;(2)连接BD、DE,若BD⊥DE,求证:四边形ABCD为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AEF,延长EF交边BC于点G,连结AG,CF,则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤S△FGC=![]() ;其中正确的结论有_____.
;其中正确的结论有_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
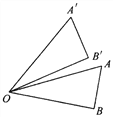
【题目】如图,Rt△AOB绕着一点旋转到△A′OB′的位置,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段和角.已知∠AOB=30°,∠AOB′=10°,那么点B的对应点是点______;线段OB的对应线段是线段_____;∠A的对应角是______;旋转中心是点_______;旋转的角度是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,三角形![]() 的三个顶点的位置如图,
的三个顶点的位置如图,![]() 为三角形
为三角形![]() 内一点,
内一点,![]() 的坐标为
的坐标为![]()
(1)平移三角形![]() ,使
,使![]() 点与原点重合,请画出平移后的三角形
点与原点重合,请画出平移后的三角形![]()
(2)直接写出![]() 的对应点
的对应点![]() 的坐标;并写出平移的规律.
的坐标;并写出平移的规律.
![]() ( , );
( , );
![]() ( , );
( , );
![]() ( , );
( , );
(3)求三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小强上山游玩,小颖乘坐缆车,小强步行,两人相约在山顶的缆车终点会和,已知小强行走到缆车终点的路程是缆车到山顶的线路长的![]() 倍,小颖在小强出发后
倍,小颖在小强出发后![]() 分才乘上缆车,缆车的平均速度为
分才乘上缆车,缆车的平均速度为![]() 米/分,若图中的折线表示小强在整个行走过程中的路程(米)与出发时间(分)之间的关系的图像,请回答下列问题.
米/分,若图中的折线表示小强在整个行走过程中的路程(米)与出发时间(分)之间的关系的图像,请回答下列问题.

(1)小强行走的总路程是 米,他途中休息了 分;
(2)分别求出小强在休息前和休息后所走的两段路程的速度;
(3)当小颖到达缆车终点时,小强离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
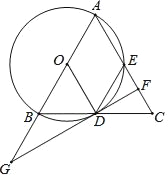
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC,AC于D,E两点,过点D作⊙O的切线,交AC于点F,交AB的延长线于点G.
(1)求证:EF=CF;
(2)若cos∠ABC=![]() ,AB=10,求线段AF的长.
,AB=10,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
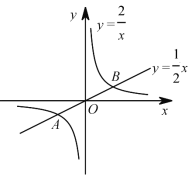
【题目】当![]() 值相同时,我们把正比例函数
值相同时,我们把正比例函数![]() 与反比例函数
与反比例函数![]() 叫做“关联函数”,可以通过图象研究“关联函数”的性质.小明根据学习函数的经验,先以
叫做“关联函数”,可以通过图象研究“关联函数”的性质.小明根据学习函数的经验,先以![]() 与
与![]() 为例对“关联函数”进行了探究.下面是小明的探究过程,请你将它补充完整.
为例对“关联函数”进行了探究.下面是小明的探究过程,请你将它补充完整.
(1)如图,在同一坐标系中画出这两个函数的图象.设这两个函数图象的交点分别为![]() ,
,![]() ,则点
,则点 ![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为_______;
的坐标为_______;
(2)点![]() 是函数
是函数![]() 在第一象限内的图象上一个动点(点
在第一象限内的图象上一个动点(点![]() 不与点
不与点![]() 重合),设点
重合),设点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() 且
且![]() .
.
①结论![]() :作直线
:作直线![]() ,
,![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
,![]() ,则在点
,则在点![]() 运动的过程中,总有
运动的过程中,总有![]() .
.
证明:设直线![]() 的解析式为
的解析式为![]() ,将点
,将点![]() 和点
和点![]() 的坐标代入,得
的坐标代入,得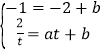
解得 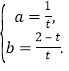 则直线
则直线![]() 的解析式为
的解析式为![]() .
.
令 ![]() ,可得
,可得![]() ,则点
,则点![]() 的坐标为
的坐标为![]() .
.
同理可求,直线![]() 的解析式为
的解析式为![]() ,点
,点![]() 的坐标为________.
的坐标为________.
请你继续完成证明![]() 的后续过程:
的后续过程:
②结论![]() :设
:设![]() 的面积为
的面积为![]() ,则
,则![]() 是
是![]() 的函数.请你直接写出
的函数.请你直接写出![]() 与
与![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com