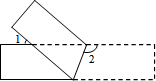
将一矩形纸条按如图所示折叠.若∠1=40°.则∠2=110°．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

3．

将一矩形纸条按如图所示折叠，若∠1=40°，则∠2=110°．

分析根据平行线的性质得到∠3=∠1=40°，∠2+∠4=180°，由折叠的性质得到∠4=∠5，即可得到结论．

解答解：∵AB∥CD，
∴∠3=∠1=40°，∠2+∠4=180°，
∵∠4=∠5，
∴∠4=∠5=$\frac{1}{2}$（180°-40°）=70°，
∴∠2=110°，
故答案为：110°．

点评本题考查了平行线的性质和折叠的知识，题目比较灵活，解答本题的关键熟练掌握平行线的性质．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

13．

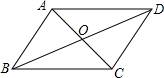如图，?ABCD的对角线AC、BD相交于点O，若AB=5，△OCD的周长为16，则AC与BD的和是（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

14．在等边△ABC中，作以DB为直角边的等腰Rt△DBC（A、D两点在BC的同侧），则∠ADB=135°．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

11．已知a=$\sqrt{5}-\sqrt{2}$，b=$\sqrt{5}+\sqrt{2}$，求$\frac{a}{b}$+$\frac{b}{a}$的值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

18．

为进一步缓解城市交通压力，义乌市政府推出公共自行车，公共自行车在任何一个网店都能实现通租通还，某校学生小明统计了周六校门口停车网点各时段的借、还自行车数，以及停车点整点时刻的自行车总数（称为存量）情况，表格中x=1时的y的值表示8：00点时的存量，x=2时的y值表示9：00点时的存量…以此类推，他发现存量y（辆）与x（x为整数）满足如图所示的一个二次函数关系．

时段	x	还车数	借车数	存量y
7：00-8：00	1	7	5	15
8：00-9：00	2	8	7	n
…	…	…	…	…

根据所给图表信息，解决下列问题：
（1）m=13，解释m的实际意义：7：00时自行车的存量；
（2）求整点时刻的自行车存量y与x之间满足的二次函数关系式；
（3）已知10：00-11：00这个时段的借车数比还车数的一半还要多2，求此时段的借车数．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

8．判断下列长度的三条线段能否组成三角形：
（1）m-2，m，2（m＞2）；
（2）x+1，x+m，2x（x＞0）；
（3）a+1，a+2，a+3（a＞0）．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

15．化简$\frac{a-b}{\sqrt{a}+\sqrt{b}}$，甲、乙两同学的解法如下：
甲：$\frac{a-b}{\sqrt{a}+\sqrt{b}}$=$\frac{（a-b）（\sqrt{a}-\sqrt{b}）}{（\sqrt{a}+\sqrt{b}）（\sqrt{a}-\sqrt{b}）}$=$\frac{（a-b）（\sqrt{a}-\sqrt{b}）}{a-b}$=$\sqrt{a}$$-\sqrt{b}$；
乙：$\frac{a-b}{\sqrt{a}+\sqrt{b}}$=$\frac{（\sqrt{a}）^{2}-（\sqrt{b}）^{2}}{\sqrt{a}+\sqrt{b}}$=$\frac{（\sqrt{a}+\sqrt{b}）（\sqrt{a}-\sqrt{b}）}{\sqrt{a}+\sqrt{b}}$=$\sqrt{a}$-$\sqrt{b}$．
对于甲、乙两同学的解法，正确的判断是（　　）