
【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1 , x2 .
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
【答案】
(1)
解:∵原方程有两个实数根,
∴△=(﹣2)2﹣4(m﹣1)≥0,
整理得:4﹣4m+4≥0,
解得:m≤2;
(2)
解:∵x1+x2=2,x1x2=m﹣1,x12+x22=6x1x2,
∴(x1+x2)2﹣2x1x2=6x1x2,
即4=8(m﹣1),
解得:m= ![]() .
.
∵m= ![]() <2,
<2,
∴符合条件的m的值为 ![]()
【解析】(1)根据一元二次方程x2﹣2x+m﹣1=0有两个实数根,可得△≥0,据此求出m的取值范围;(2)根据根与系数的关系求出x1+x2 , x1x2的值,代入x12+x22=6x1x2求解即可.本题考查了根与系数的关系以及根的判别式,解答本题的关键是掌握两根之和与两根之积的表达方式.
【考点精析】本题主要考查了求根公式和根与系数的关系的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商才能正确解答此题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,点D,E分别在AC,BC上,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若PF=3,则BP=( )
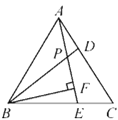
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在△ABC中,以AB、AC为直角边, 分别向外作等腰直角三角形ABE、ACF,连结EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.
(1)用圆规比较EM与FM的大小.
(2)你能说明由(1)中所得结论的道理吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,不正确的是![]()
![]()
![]() 全等形的面积相等;
全等形的面积相等;
![]() 形状相同的两个三角形是全等三角形;
形状相同的两个三角形是全等三角形;
![]() 全等三角形的对应边,对应角相等;
全等三角形的对应边,对应角相等;
![]() 若两个三角形全等,则其中一个三角形一定是由另一个三角形旋转得到的.
若两个三角形全等,则其中一个三角形一定是由另一个三角形旋转得到的.
A. ![]() 与
与![]() B.
B. ![]() 与
与![]() C.
C. ![]() 与
与![]() D.
D. ![]() 与
与![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:![]() 形状相同的图形是全等形;
形状相同的图形是全等形;![]() 全等形的大小相同,形状也相同;
全等形的大小相同,形状也相同;![]() 全等三角形的面积相等;
全等三角形的面积相等;![]() 面积相等的两个三角形全等;
面积相等的两个三角形全等;![]() 若
若![]() ≌
≌![]() ,
,![]() ≌
≌![]() ,则
,则![]() ≌
≌![]() 其中正确的说法有
其中正确的说法有![]()
![]()
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.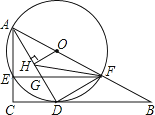
(1)求证:AD平分∠CAB;
(2)若OH⊥AD于点H,FH平分∠AFE,DG=1.
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段 AB=24,动点 P 从 A 出发,以每秒 2 个单位的速度沿射线 AB运动,运动时间为 t 秒(t>0),M 为 AP 的中点.
(1)当点 P 在线段 AB 上运动时,
①当 t 为多少时,PB=2AM?②求2BM-BP的值.
(2)当 P 在 AB 延长线上运动时,N 为 BP 的中点,说明线段 MN 的长度不变,并 求出其值.
(3)在 P 点的运动过程中,是否存在这样的 t 的值,使 M、N、B 三点中的一个点 是以其余两点为端点的线段的中点,若有,请求出 t 的值;若没有,请说明理 由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8 分)2013 年 4 月起泉州市区居民生活用水开始实行阶梯式计量水价,据了解,此次实行的阶梯式计量水价分为三级(如表所示):

例:若某用户 2013 年 6 月份的用水量为 35 吨,按三级计算则应交水费为:
20×1.65+(30﹣20)×2.48+(35﹣30)×3.30=74.3(元)
(1)如果小东家 2013 年 6 月份的用水量为 20 吨,则需缴交水费多少元?
(2)如果小明家 2013 年 7 月份的用水量为 a 吨,水价要按两级计算,则小明家该月应缴交水费多少元?(用含 a 的代数式表示,并化简)
(3)若一用户 2013 年 7 月份应该水费 90.8 元,则该户人家 7 月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为米.(结果保留根号)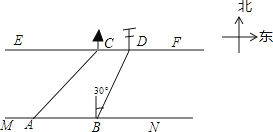
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com