
����Ŀ����֪��ABC�DZ߳�Ϊ4�ĵȱ������Σ���AB������OM�ϣ���OA��6����D������OM�ϵĶ��㣬����D�����A�غ�ʱ������ACD�Ƶ�C��ʱ�뷽����ת60��õ���BCE������DE����OD��m��
(1)���ⷢ��
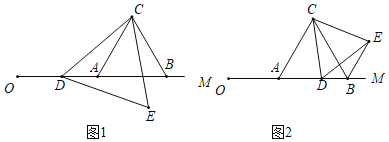
��ͼ1����CDE����״���� �������Σ�
(2)̽��֤��
��ͼ2����6��m��10ʱ����BDE���ܳ��Ƿ������Сֵ�������ڣ������BDE�ܳ�����Сֵ���������ڣ���˵�����ɣ�
(3)�������
�Ƿ����m��ֵ��ʹ��DEB��ֱ�������Σ������ڣ���ֱ��д��m��ֵ���������ڣ���˵�����ɣ�
���𰸡�(1)�ȱߣ�(2)���ڣ���6��t��10ʱ����BDE����С�ܳ�2![]() +4��(3)��m��2��14ʱ����D��E��BΪ�������������ֱ�������Σ�
+4��(3)��m��2��14ʱ����D��E��BΪ�������������ֱ�������Σ�
��������
��1������ת�����ʵõ���DCE��60����DC��EC�����ɵõ����ۣ�
��2����6��m��10ʱ������ת�����ʵõ�BE��AD�����ǵõ�C��DBE��BE+DB+DE��AB+DE��4+DE�����ݵȱ������ε����ʵõ�DE��CD���ɴ��߶���̵õ���CD��ABʱ����BDE���ܳ���С�����ǵõ����ۣ�
��3�����ڣ��ٵ���D���B�غ�ʱ��D��B��E���ܹ��������Σ�
�ڵ�0��m��6ʱ������ת�����ʵõ���ABE��60������BDE��60������á�BED��90�������ݵȱ������ε����ʵõ���DEB��60������á�CEB��30�������OD��OA��DA��6��4��2��m
�۵�6��m��10ʱ����ʱ�����ڣ�
�ܵ�m��10ʱ������ת�����ʵõ���DBE��60������á�BDE��60�������ǵõ�m��14��
(1)�߽���ACD�Ƶ�C��ʱ�뷽����ת60���õ���BCE��
���DCE��60����DC��EC��
���CDE�ǵȱ������Σ�
�ʴ�Ϊ���ȱߣ�
(2)���ڣ���6��t��10ʱ��
����ת�����ʵã�BE��AD��
��C��DBE��BE+DB+DE��AB+DE��4+DE��
��(1)֪����CDE�ǵȱ������Σ�
��DE��CD��
��C��DBE��CD+4��
�ɴ��߶���̿�֪����CD��ABʱ����BDE���ܳ���С��
��ʱ��![]()
���BDE����С�ܳ�![]()
(3)���ڣ��١ߵ���D���B�غ�ʱ��D��B��E���ܹ��������Σ�
�൱��D���B�غ�ʱ�����������⣬
�ڵ�0��m��6ʱ������ת��֪����ABE��60������BDE��60����
���BED��90����
��(1)��֪����CDE�ǵȱ������Σ�
���DEB��60����
���CEB��30����
�ߡ�CEB����CDA��
���CDA��30����
�ߡ�CAB��60����
���ACD����ADC��30����
��DA��CA��4��
��OD��OA��DA��6��4��2��
��m��2��
�۵�6��m��10ʱ���ɡ�DBE��120����90����
���ʱ�����ڣ�
�ܵ�m��10ʱ������ת�����ʿ�֪����DBE��60����
����(1)֪��CDE��60����
���BDE����CDE+��BDC��60��+��BDC��
����BDC��0����
���BDE��60����
��ֻ�ܡ�BDE��90����
�Ӷ���BCD��30����
��BD��BC��4��
��OD��14��
��m��14��
������������m��2��14ʱ����D��E��BΪ�������������ֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��x�ᣬy��ֱ��ڵ�A��2��0������B��0��2![]() ��������D��1����λ����/����ٶȴӵ�A������x�Ḻ�����˶���ͬʱ����E��
��������D��1����λ����/����ٶȴӵ�A������x�Ḻ�����˶���ͬʱ����E��![]() ����λ����/����ٶȴӵ�B������y�Ḻ�����˶������˶�ʱ��Ϊt�룬�Ե�AΪ����������߾�����E������E��x���ƽ���ߣ��������ߵ���һ������Ϊ��G����AB�ཻ�ڵ�F
����λ����/����ٶȴӵ�B������y�Ḻ�����˶������˶�ʱ��Ϊt�룬�Ե�AΪ����������߾�����E������E��x���ƽ���ߣ��������ߵ���һ������Ϊ��G����AB�ཻ�ڵ�F
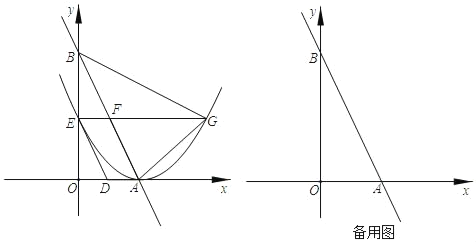
��1�����OAB������
��2����tΪ��ֵʱ���ı���ADEFΪ���Σ��������ʱ���κ�������ʽ��
��3���Ƿ����ʵ��t��ʹ��AGFΪֱ�������Σ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ��ڡ�O��AC��ֱ������D��AC�ӳ�����һ�㣬�ҡ�DBC����BAC��![]() ��
��
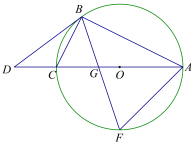
��1����֤��BD�ǡ�O�����ߣ���2����![]() ��ֵ����3����ͼ��ֱ��AC=5��
��ֵ����3����ͼ��ֱ��AC=5��![]() �����ABF�����
�����ABF�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�˿�ѧ������ѧ�������ɳ��������������ȡ�˲���ѧ����ͥ����ҳ�����������Ϊ����ĩ�����ڼ��������������ʾ����飬�����յ��ʾ����з����������õ������µ�����ͳ�Ʊ�������ͳ��ͼ��
���� | ������� | ��ͥ�� |
| �������沢�ҹ�������ҵ������ | 16 |
| ֻ��������ҵ������ | b |
| ֻ�������� | 8 |
| �Ȳ���������Ҳ����������ҵ������ | d |
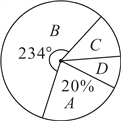
��1����![]() ��ֵ��
��ֵ��
��2����Уѧ����ͥ����Ϊ500��ѧУ������������![]() ���ͥ�г�ȡ�ҳ������ѵ�࣬�����Ϊ
���ͥ�г�ȡ�ҳ������ѵ�࣬�����Ϊ![]() ��ȡ20%��
��ȡ20%��![]() ���ȡ60%��������Ƹ���ѵ��ļ�ͥ����
���ȡ60%��������Ƹ���ѵ��ļ�ͥ����
��3������![]() ���ͥ��ֻ��һ�������ͥ��������ũ���ͥ�������оٷ������
���ͥ��ֻ��һ�������ͥ��������ũ���ͥ�������оٷ������![]() ����������2����ͥ������Ȳɷã�������һ���dz����ͥ�ĸ��ʣ�
����������2����ͥ������Ȳɷã�������һ���dz����ͥ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AB=6��BC=12����E�ڱ�BC�ϣ���BE=2CE���������ع���E��ֱ���۵�����C��D�Ķ�Ӧ��ֱ�ΪC�䣬D�����ۺ����AD���ڵ�F������B��C�䣬D��ǡ����ͬһֱ����ʱ��AF�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
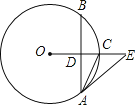
����Ŀ����ͼ������O�У��뾶OC��ֱ����AB������Ϊ��D����E��OC���ӳ����ϣ���EAC����BAC
(1)��֤��AE����O�����ߣ�
(2)��AB��8��cosE��![]() ����CD�ij���
����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������⣬��ͬ���ڽǻ���������x2��4����x��2����![]() ����ƽ���ҵ�ֱ����ֱ���ң��ݵȻ����Ե�Բ�Ľ���ȣ�����ȵ�Բ�Ľ����ԵĻ���ȣ�����������������������ȡһ��������������ĸ���Ϊ_____��
����ƽ���ҵ�ֱ����ֱ���ң��ݵȻ����Ե�Բ�Ľ���ȣ�����ȵ�Բ�Ľ����ԵĻ���ȣ�����������������������ȡһ��������������ĸ���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
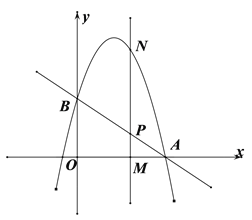
����Ŀ����ͼ��ֱ��![]() ��x�ύ�ڵ�
��x�ύ�ڵ�![]() ����y�ύ�ڵ�B��������
����y�ύ�ڵ�B��������![]() ������
������![]() ��
��
![]() ��k��ֵ�������ߵĽ���ʽ��
��k��ֵ�������ߵĽ���ʽ��
![]() Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ����ֱ��AB�������߷ֱ��ڵ�
Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ����ֱ��AB�������߷ֱ��ڵ�![]() ��
��
![]() ����O,B,N,PΪ������ı���OBNP��ƽ���ı���ʱ,��m��ֵ.
����O,B,N,PΪ������ı���OBNP��ƽ���ı���ʱ,��m��ֵ.
![]() ��
��![]() ʱ,��m��ֵ.
ʱ,��m��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲���������������A��B����֮��ľ��룬����ʵ�������������ͼ��ʾ��ͼ�Σ�����AB��BE��EF��BE��AF��BE�ڵ�D��C��BD�ϣ�����λͬѧ�ֱ�����������������ݣ���BC����ACB����CD����ACB����ADB����EF��DE��BD����DE��DC��BC.�ܸ����������ݣ����A��B��������( )
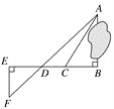
A. 4��B. 3��C. 2��D. 1��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com