
【题目】下列方程变形中,正确的是( )
A.方程3x-2=2x+1,移项,得3x-2x=1-2
B.方程3-x=2-5(x-1),去括号,得3-x=2-5x-1;
C.方程-75x=76,方程两边同除以-75,得x=-![]()
D.方程![]() =1+
=1+![]() ,去分母,得2(2x-1)=6+3(x-3)
,去分母,得2(2x-1)=6+3(x-3)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A. 2,![]() B. 2,1 C. 4,
B. 2,1 C. 4,![]() D. 4,3
D. 4,3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b为有理数,且a,b不为0,则定义有理数对(a,b)的“真诚值”为d(a,b)= ,如有理数对(3,2)的“真诚值”为d(3,2)=23﹣10=﹣2,有理数对(﹣2,5)的“真诚值”为d(﹣2,5)=(﹣2)5﹣10=﹣42.
,如有理数对(3,2)的“真诚值”为d(3,2)=23﹣10=﹣2,有理数对(﹣2,5)的“真诚值”为d(﹣2,5)=(﹣2)5﹣10=﹣42.
(1)求有理数对(﹣3,2)与(1,2)的“真诚值”;
(2)求证:有理数对(a,b)与(b,a)的“真诚值”相等;
(3)若(a,2)的“真诚值”的绝对值为|d(a,2)|,若|d(a,2)|=6,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,边CO在x轴正半轴上,∠AOC=60°,反比例函数y=![]() (x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )
(x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )

A. 1 B. ![]() C. 2
C. 2![]() ﹣
﹣![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小莉的爸爸买了今年七月份去上海看世博会的一张门票,她和哥哥两人都很想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将数字为1,2,3,5的四张牌给小莉,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,如果和为偶数,则小莉去;如果和为奇数,则哥哥去.
(1)请用数状图或列表的方法求小莉去上海看世博会的概率;
(2)哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
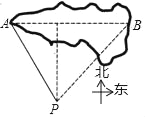
【题目】在数学活动课上,九年级(1)班数学兴趣小组的同学们要测量某公园人工湖亭子A与它正东方向的亭子B之间的距离,现测得亭子A位于点P北偏西30°方向,亭子B位于点P北偏东42°方向,测得点P与亭子A之间的距离为200米,求亭子A与亭子B之间的距离.(结果精确到1米)
【参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90, ![]() =1.73】
=1.73】
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定:抛物线y=a(x﹣h)2+k的关联直线为y=a(x﹣h)+k.
例如:抛物线y=2(x+1)2﹣3的关联直线为y=2(x+1)﹣3,即y=2x﹣1.
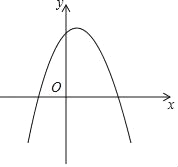
(1)如图,对于抛物线y=﹣(x﹣1)2+3.
①该抛物线的顶点坐标为_____,关联直线为_____,该抛物线与其关联直线的交点坐标为_____和_____;
②点P是抛物线y=﹣(x﹣1)2+3上一点,过点P的直线PQ垂直于x轴,交抛物线y=﹣(x﹣1)2+3的关联直线于点Q.设点P的横坐标为m,线段PQ的长度为d(d>0),求当d随m的增大而减小时,d与m之间的函数关系式,并写出自变量m的取值范围.
(2)顶点在第一象限的抛物线y=﹣a(x﹣1)2+4a与其关联直线交于点A,B(点A在点B的左侧),与x轴负半轴交于点C,直线AB与x轴交于点D,连结AC、BC.
①求△BCD的面积(用含a的代数式表示).
②当△ABC为钝角三角形时,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用1块A型钢板可制成2个C型模具和1个D型模具;用1块B型钢板可制成1个C型模具和3个D型模具,现准备A、B型钢板共100块,并全部加工成C、D型模具.
(1)若B型钢板的数量是A型钢板的数量的两倍还多10块,求A、B型钢板各有多少块?
(2)若销售C、D型模具的利润分别为80元/块、100元/块,且全部售出.
①当A型钢板数量为25块时,那么共可制成C型模具 个,D型模具 个;
②当C、D型模具全部售出所得的利润为34400元,求A型钢板有多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程
(1)(x﹣5)2=16(直接开平方法) (2)x2﹣4x+1=0(配方法)
(3)x2+3x﹣4=0(公式法) (4)x2+5x﹣3=0(配方法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com