

分析 (1)证明四边形AFDE是平行四边形,且△DCF和△BDF是等腰三角形即可证得;
(2)根据(1)中的结论代入数据直接求解.
解答 解:(1)图②③中:AC+DF=DE.
证明:图②结论:
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴AF=DE.
∵DE∥AC,
∴∠CDF=∠B,
又∵AB=AC,
∴∠B=∠ACB,
∴∠CDF=∠ACB,
∵∠ACB=∠DCF,
∴∠CDF=∠DCF,
∴DF=CF,
∴AC+DF=AF=DE;
同理可证出图③结论:AC+DF=AF=DE.
(2)当如图①的情况,DF=AC-DE=6-4=2;
当如图②③的情况,DF=DE-AC=4-6=-2(舍去).
故答案为:2.
点评 本题考查了平行线的性质、等腰三角形的性质依据平行线的判定及性质,解题的关键是:(1)证出AC+DF=AF=DE;(2)代入数据直接求解.本题属于中档题,难度不大,解决该题型题目时,根据平行四边形的判定即性质找出相等的边角关系是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
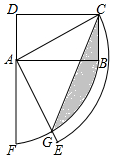 如图矩形ABCD中,AD=1,CD=$\sqrt{3}$,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为$\frac{π}{2}$-$\frac{\sqrt{3}}{2}$.
如图矩形ABCD中,AD=1,CD=$\sqrt{3}$,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为$\frac{π}{2}$-$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)请在横线上填写合适的内容,完成下面的证明:
(1)请在横线上填写合适的内容,完成下面的证明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com