
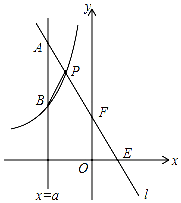 如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{4}{x}$
如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{4}{x}$分析 (1)先确定出点P的坐标,再利用待定系数法即可得出结论;
(2)①先判断出△APB∽△FOE,用得出的比例式建立方程求解即可;
②利用线段的中点坐标建立方程求解即可得出结论.
解答 解:(1)∵点P(-1,n)在反比例函数y=-$\frac{4}{x}$图象上,
∴n=4,
∴P(-1,4),
∵F是PE的中点,
∴F(0,2),
∴$\left\{\begin{array}{l}{-k+b=4}\\{b=2}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$,
∴y=-2x+2.
(2)①∵△ABP是以点P为直角顶点的直角三角形,
∴∠APB=90°=∠EOF,
∵直线AB∥y轴,
∴∠BAP=∠OFE,
∴△APB∽△FOE,
∴$\frac{AP}{OF}$=$\frac{AB}{EF}$
当x=a时,y=-2a+2,
∴A(a,-2a+2),
∵P(-1,4),
∴AP=$\sqrt{(a+1)^{2}+(-2a+2-4)^{2}}$=$\sqrt{5(a+1)^{2}}$=$\sqrt{5}$|a+1|
当x=a时,y=-$\frac{4}{a}$,
∴B(a,-$\frac{4}{a}$),
∴AB=|-2a+2+$\frac{4}{a}$,
∵直线EF的解析式为y=-2x+2,
∴E(1,0),F(0,2),
∴OF=2,EF=$\sqrt{5}$,
∴$\frac{\sqrt{5}|a+1|}{2}=\frac{|-2a+2+\frac{4}{a}|}{\sqrt{5}}$,
∴a=$\frac{8}{9}$(舍)或a=-1(舍)或a=-8,
即:a=-8时,△ABP是以点P为直角顶点的直角三角形;
②如图,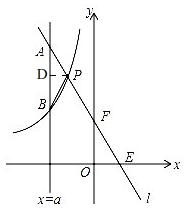
过P作PD⊥AB,垂足为点D,
∵P(-1,4),
∴D点的纵坐标为4,
∵PA=PB,
∴点D为AB的中点,
由题意知,A点的纵坐标为-2a+2,B点的纵坐标为$-\frac{4}{a}$,
∴$-2a+2-\frac{4}{a}=4×2$,
解得a1=-2,a2=-1(舍去).
∴当a=-2时,PA=PB.
点评 此题是反比例函数综合题,主要考查了待定系数法,相似三角形的判定和性质,线段中点坐标的确定方法,解(1)的关键是掌握待定系数法,解(2)①的关键是判断出△APB∽△FOE,解(3)的关键是用线段的中点坐标公式建立方程,是一道基础题目.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在正方形ABCD中,点E在BC的延长线上,且CE=CD,点F为DE边上一点,连接AF,作FG⊥AF交直线DC于点G
在正方形ABCD中,点E在BC的延长线上,且CE=CD,点F为DE边上一点,连接AF,作FG⊥AF交直线DC于点G查看答案和解析>>
科目:初中数学 来源: 题型:解答题
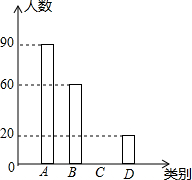
 某区为了解七年级学生开展跳绳活动的情况,随机调查了该区部分学校七年级学生1分钟跳绳的次数,将调查结果进行统计,下面是根据调查数据制作的统计图表的一部分.
某区为了解七年级学生开展跳绳活动的情况,随机调查了该区部分学校七年级学生1分钟跳绳的次数,将调查结果进行统计,下面是根据调查数据制作的统计图表的一部分.| 分组 | 次数x(个) | 人数 |
| A | 0≤x<120 | 24 |
| B | 120≤x<130 | 72 |
| C | 130≤x<140 | |
| D | x≥140 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
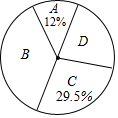
 雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康.在2017年2月周末休息期间,某校九年级一班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计表及统计图,观察并回答下列问题:
雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康.在2017年2月周末休息期间,某校九年级一班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计表及统计图,观察并回答下列问题:| 类别 | 雾霾天气的主要成因 | 百分比 |
| A | 工业污染 | 45% |
| B | 汽车尾气排放 | m |
| C | 城中村燃煤问题 | 15% |
| D | 其他(绿化不足等) | n |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com