
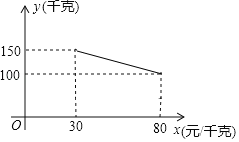
����Ŀ��ij��������һ����Ʒ���ɱ���Ϊ20Ԫ/ǧ�ˣ����г����飬ÿ��������y(ǧ��)�����۵���x(Ԫǧ��)֮��Ĺ�ϵ��ͼ��ʾ���涨ÿǧ���ۼ۲��ܵ���30Ԫ���Ҳ�����80Ԫ��
(1)ֱ��д��y��x֮��ĺ�����ϵʽ��
(2)����ó�������������Ʒÿ����3900Ԫ��������ô����Ʒ�����۵���Ϊ����Ԫ��
(3)��ÿ���������ΪwԪ�������۵��۶�Ϊ����Ԫʱ���ó���ÿ������������������Ƕ���Ԫ��
���𰸡�(1)y����x+180��(2)����Ʒ�����۵���Ϊ50Ԫ��(3)���۵��۶�Ϊ80Ԫʱ���ó���ÿ�����������������6000Ԫ��
��������
��1�����㣨30��150������80��100������һ�κ�������ʽ��������⣻
��2��������ã���x20����x��180����3900��������⣻
��3��������ã�w����x20����x��180������x100��2��6400��������⣮
�⣺(1)����(30��150)��(80��100)����һ�κ�������ʽ�ã�![]() ��
��
��ã�![]() ��
��
�ʺ����ı���ʽΪ��y����x+180��
(2)������ã�(x��20)(��x+180)��3900��
��ã�x��50��150(��ȥ150)��
�ʣ�����Ʒ�����۵���Ϊ50Ԫ��
(3)������ã�w��(x��20)(��x+180)����(x��100)2+6400��
�ߩ�1��0���ʵ�x��100ʱ��W��x�����������30��x��80��
�൱x��80ʱ��W�����ֵ����ʱ��w��6000��
�����۵��۶�Ϊ80Ԫʱ���ó���ÿ�����������������6000Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
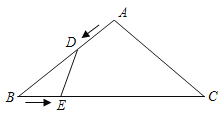
����Ŀ����ͼ��ʾ���ڵ�����ABC�У�AB��AC��10cm��BC��16cm����D�ɵ�A������AB�������B�����˶���ͬʱ��E�ɵ�B������BC�������C�����˶������ǵ��ٶȾ�Ϊ1cm/s������DE�����˶�ʱ��Ϊt��s����0��t��10��������������⣺
��1����tΪ��ֵʱ����BDE�����Ϊ7.5cm2��
��2���ڵ�D��E���˶��У��Ƿ����ʱ��t��ʹ�á�BDE���ABC���ƣ������ڣ��������Ӧ��ʱ��t���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ABCD�У�AB��5��BC��8����PΪBC��һ���㣨����˵��غϣ�������AP������ABP����AP�۵�����B�䵽M��������BM��CM������BMCΪ���������Σ���BP�ij���Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
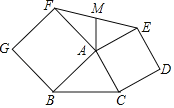
����Ŀ����֪����ͼ���ڡ�ABC�У�cos��ABC��![]() ��sin��ACB��
��sin��ACB��![]() ��AC��2���ֱ���AB��ACΪ�����ABC������������ABGF��������ACDE������EF����M��EF���е㣬����AM�����AEF�����Ϊ_____��AM�ij�Ϊ_____��
��AC��2���ֱ���AB��ACΪ�����ABC������������ABGF��������ACDE������EF����M��EF���е㣬����AM�����AEF�����Ϊ_____��AM�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ӽ�����ij���о��꼶1200��ѧ�������ѡȡһ����ѧ�����е��飬���������A������ʱ����1Сʱ��B��1Сʱ������ʱ����4Сʱ��C��4Сʱ������ʱ����7Сʱ��D������ʱ�䣾7Сʱ��ͳ�ƽ���Ƴ�����ͼͳ��ͼ�����½�������ȷ�ĸ����ǣ� ��
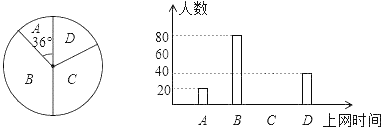
�ٲμӵ����ѧ����200�ˣ�
�ڹ���У����������7Сʱ��ѧ��������900��
��C��������60�ˣ�
��D���Ե�Բ�Ľ���72����
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ݹ�˾Ϊ��߿�ݷּ���ٶȣ���������������������˹��ּ������ͺŵĻ����˵Ĺ���Ч�ʺͼ۸������
�ͺ� | �� | �� |
ÿ̨ÿСʱ�ּ��ݼ���(��) | 1000 | 800 |
ÿ̨�۸�(��Ԫ) | 5 | 3 |
�ù�˾�ƻ������������ͺŵĻ����˹�10̨������ʹ��10̨������ÿСʱ�ּ��ݼ����ܺͲ�����8500��
(1)�蹺������ͺŵĻ�����x̨��������10̨�����������ķ���Ϊy��Ԫ����y��x֮��Ĺ�ϵʽ��
(2)����̨�����ͺŵĻ����ˣ���ʹ������10̨�����������ܷ������٣����ٷ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˹��������ܱߵ�ũ����ֲ˵Ļ����ԣ�ij��˾�ƻ��½�![]() ��
��![]() ��������80���������۸�ũ���ֲˣ���֪��1��
��������80���������۸�ũ���ֲˣ���֪��1��![]() �����Һ�2��
�����Һ�2��![]() ������һ����Ҫ8.1��Ԫ���������ҵijɱ��ͳ��ۼ����±���
������һ����Ҫ8.1��Ԫ���������ҵijɱ��ͳ��ۼ����±���
|
| |
�ɱ�����Ԫ/���� | 2.5 |
|
���ۼۣ���Ԫ/���� | 3.1 | 3.5 |
��1����![]() ��ֵ��
��ֵ��
��2����֪�½�![]() �����Ҳ�����38��������50�����������������ҿ�ȫ���۳���Ϊ�˼����ũ���������ʲ���ʲô�����������ҿ�ʹ�������٣����������Ƕ��٣�
�����Ҳ�����38��������50�����������������ҿ�ȫ���۳���Ϊ�˼����ũ���������ʲ���ʲô�����������ҿ�ʹ�������٣����������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
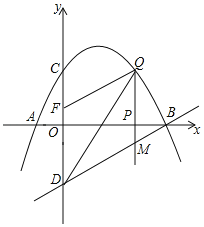
����Ŀ����ͼ����֪������y����![]() +bx+c��ͼ����A(��1��0)�͵�C(0��2)����D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ(m��0)������P��x��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M.
+bx+c��ͼ����A(��1��0)�͵�C(0��2)����D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ(m��0)������P��x��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M.
(1)�������������ʾ�Ķ��κ����ı���ʽ.
(2)��֪��F(0��![]() )������P��x�����������˶�ʱ������mΪ��ֵʱ���ı���DMQF��ƽ���ı��Σ�
)������P��x�����������˶�ʱ������mΪ��ֵʱ���ı���DMQF��ƽ���ı��Σ�
(3)��P���߶�AB�˶������У��Ƿ���ڵ�Q��ʹ���Ե�B��Q��MΪ��������������BOD���ƣ������ڣ������Q�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com