
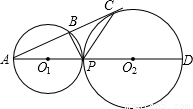
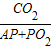 ,则当⊙O1、⊙O2的半径分别为2cm、3cm时,当⊙O1、⊙O2的半径分别为4cm、6cm时,sin∠BAP的值均可求.由此易得sin∠BAP=
,则当⊙O1、⊙O2的半径分别为2cm、3cm时,当⊙O1、⊙O2的半径分别为4cm、6cm时,sin∠BAP的值均可求.由此易得sin∠BAP=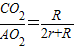 .
. (1)证明:连接CO2、CD,
(1)证明:连接CO2、CD,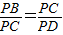 .
.
 .
.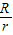 的值唯一确定sin∠BAP的值.
的值唯一确定sin∠BAP的值.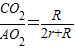 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
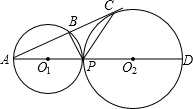 cm时,sin∠BAP的值是多少?分析sin∠BAP值的变化,你能发现什么规律?请尝试证明或否定你的猜想.
cm时,sin∠BAP的值是多少?分析sin∠BAP值的变化,你能发现什么规律?请尝试证明或否定你的猜想.查看答案和解析>>
科目:初中数学 来源:第24章《圆(下)》中考题集(33):24.3 圆和圆的位置关系(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第7章《锐角三角函数》中考题集(06):7.2 正弦、余弦(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第28章《圆》中考题集(50):28.2 与圆有关的位置关系(解析版) 题型:解答题
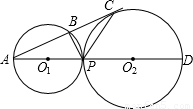
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com