
分析 根据两数的最小公倍数的意义及求法、最大公因数的意义及求法,弄清数量关系,设出这两个数,然后进行推理求解.
解答 解:设a、b两数的最大公约数M,令两数为a=AM、b=BM,AB互质,最小公倍数为ABM
AM+BM=(A+B)M=432=24×33 …①
ABM+M=(AB+1)M=7776=25×35 …②
则②÷①得(AB+1)÷(A+B)=2×32=18
AB+1=18A+18B
等式右为偶数,则AB奇数,则A、B必然同为奇数.
(B-18)A=18B-1
A=(18B-1)÷(B-18)=(18B-324+323)÷(B-18)=18+323÷(B-18)
323=17×19 能被B-18整除,则有:
①B-18=17,B=35,A=37
或B-18=19,B=37,A=35
M=432÷(35+37)=6
两个数就是 a=35×6、b=37×6
或交换顺序两个数的乘积=35×6×37×6=(7776-6)×6=46620
②B-18=323,B=341,A=1
M=432÷(323+1)不为整数,舍弃
综上,ab两个数是210、222,其乘积为46620.
答:a和b的乘积是46620,
故答案为:46620.
点评 此题解题的关键是理解题意,弄清数量间的关系,明确最大公约数和最小公倍数的含义,进而推理计算得出结论.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
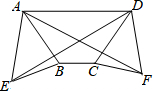 如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连AF,DE.求证:AF=DE.
如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连AF,DE.求证:AF=DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com