
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A,B是数轴上的点,请参照图并思考,完成下列各题.
![]()
(1) 若点A表示数![]() ,当点A向_____ 移动_____个单位长度时,所表示的数恰好是4的相反数.
,当点A向_____ 移动_____个单位长度时,所表示的数恰好是4的相反数.
(2) 若点A表示数![]() ,点B表示数4,当点B不动时,点A向_____移动_____个单位长度或向_____移动_____个单位长度,此时A,B两点间的距离是6.
,点B表示数4,当点B不动时,点A向_____移动_____个单位长度或向_____移动_____个单位长度,此时A,B两点间的距离是6.
(3) 若点A表示数2,将A点向左移动6个单位长度,再向右移动3个单位长度后到达点B,则B表示的数是________,此时 A,B两点间的距离是________.
(4)若A点表示数为a,将A点向右移动b个单位长度,再向左移动c个单位长度后到达点B,则点B表示的数是_____.
【答案】左. 3. 左. 1. 右. 11. -1. 3. a+b-c.
【解析】
(1)-1到-4应向左移动3个单位;
(2)先根据距离为6计算出点A的终点位置,再得出点A的平移方式;
(3)B表示的数是2-6+3,再求出 A、B两点之间的距离;
(4)B表示的数是a+b-c.
解:(1)∵ -4-(-1)=-3
∴点A向左移动3个单位长度时,所表示的数恰好是4的相反数;
(2) ∵4+6=10或4-6=-2,
∴10-(-1)=11或-2-(-1)=-1
∴点A向右移动11个单位长度到达10或向左移动1个单位长度到达-2,此时A,B两点间的距离是6.
(3) ∵2-6+3=-1
∴B表示的数是-1,
∴AB=2-(-1)=3.
(4)点B表示的数是a+b-c.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】司机小王沿东西大街跑出租车,约定向东为正,向西为负,某天自![]() 地出发到收工时,行走记录为(单位:千米):+8、-9、+7、-12、+5、-10、+17、-13.
地出发到收工时,行走记录为(单位:千米):+8、-9、+7、-12、+5、-10、+17、-13.
回答下列问题:
(1)收工时小王在![]() 地的哪边?距
地的哪边?距![]() 地多少千米?
地多少千米?
(2)若每千米耗油0.2升,问从![]() 地出发到收工时,共耗油多少升?
地出发到收工时,共耗油多少升?
(3)在工作过程中,小王最远离![]() 地多远?在
地多远?在![]() 地哪边?
地哪边?
查看答案和解析>>
科目:初中数学 来源: 题型:
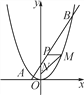
【题目】如图,已知一条直线过点(0,4),且与抛物线y=![]() x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.
(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
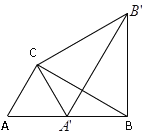
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,AC=2cm.现在将△ABC绕点C逆时针旋转至△A′B′C′,使得点A′恰好落在AB上,连接BB′,则BB′的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为32,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
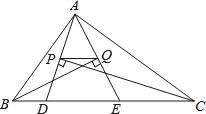
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践探究题
(1)观察下列有规律的数:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …根据规律可知
…根据规律可知
①第10个数是________; ![]() 是第________个数.
是第________个数.
②计算![]() ________.(直接写出答案即可)
________.(直接写出答案即可)
(2)![]() 是不为1的有理数,我们把
是不为1的有理数,我们把![]() 称为
称为![]() 的差倒数.如:2的差倒数是
的差倒数.如:2的差倒数是![]() ,
,![]() 的差倒数是
的差倒数是![]() .已知
.已知![]() ,
,![]() 是
是![]() 的差倒数,
的差倒数,![]() 是
是![]() 的差倒数,
的差倒数,![]() 是
是![]() 的差倒数,…,依此类推,
的差倒数,…,依此类推,![]() 是
是![]() 的差倒数,则
的差倒数,则![]() ________.
________.
(3)高斯函数[x],也称为取整函数,即[x]表示不超过x的最大整数.
例如:[2.3]=2,[-1.5]=-2.则下列结论:①[-2.1]+[1]=-2; ②[x]+[-x]=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜜蜂是自然界神奇的“建筑师“,它能用最少的材料造成最牢固的建筑物“蜂窝“,观察下列的“蜂窝图
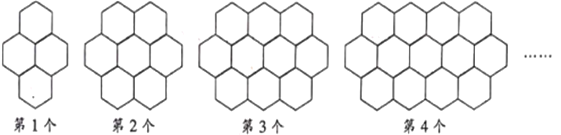
(1)若“![]() ”中每条边看成1个建筑单位,则第1个图形中共有19个建筑单位,第2个图案中共有_____个建筑单位;第3个图案中共有_____个建筑单位.
”中每条边看成1个建筑单位,则第1个图形中共有19个建筑单位,第2个图案中共有_____个建筑单位;第3个图案中共有_____个建筑单位.
(2)第n个图案中共有多少个建筑单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
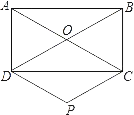
【题目】已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,过点C,D分别作BD,AC的平行线,两线相交于点P.
(1)求证:四边形CODP是菱形;
(2)当矩形ABCD的边AD,DC满足什么关系时,菱形CODP是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,在正方形ABCD中,M是AB的中点,E是AB的延长线上一点,MN⊥DM,且交∠CBE的平分线于点N.
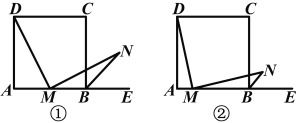
(1)求证:MD=MN;
(2)若将上述条件中“M是AB的中点”改成“M是AB上任意一点”,其余条件不变,如图②所示,则结论“MD=MN”还成立吗?若成立,给出证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com