考点:圆心角、弧、弦的关系,等腰三角形的判定与性质
专题:证明题
分析:连接AC,BD,根据∠AOB=90°得出∠AOC的度数,由等腰三角形的性质求出∠OFE的度数.根据SAS定理得出△ACO≌△DCO,故可得出∠ACO=∠OCD,根据等角对等边可得出AC=AE,同理可得BF=BD,由此可得出结论.
解答: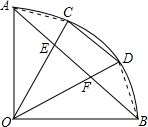
证明:连接AC,BD,
∵在⊙O中,半径OA⊥OB,C、D为弧AB的三等分点,
∴∠AOC=
∠AOB=
×90°=30°.
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠AOC=∠BOD=30°,
∴∠OEF=∠OAB+∠AOC=45°+30°=75°,同理∠OFE=75°,
∵C,D是
的三等分点,
∴AC=CD=BD,
在△ACO与△DCO中,
,
∴△ACO≌△DCO(SAS),
∴∠ACO=∠OCD.
∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD=
=75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC.
∴AC=AE,
同理,BF=BD.
又∵AC=CD=BD
∴AE=BF=CD.
点评:本题考查的是圆心角、弧、弦的关系,熟知在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等是解答此题的关键.

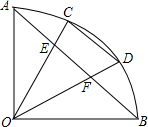 如图,∠AOB=90°,CD是
如图,∠AOB=90°,CD是
 证明:连接AC,BD,
证明:连接AC,BD,


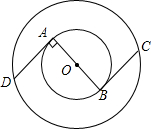 如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=
如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=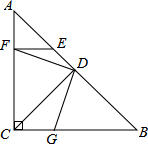 已知在△ABC中,∠ACB=90°,AC=BC,CD⊥AB,垂足为D,E是AB上一点,EF⊥AC,垂足为F,G是BC上一点,CG=EF,求证:DF=DG.
已知在△ABC中,∠ACB=90°,AC=BC,CD⊥AB,垂足为D,E是AB上一点,EF⊥AC,垂足为F,G是BC上一点,CG=EF,求证:DF=DG.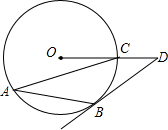 如图,AB、AC是⊙O的两条弦,过点B的切线与OC的延长线交于点D,若∠D=36°,则∠CAB的度数为( )
如图,AB、AC是⊙O的两条弦,过点B的切线与OC的延长线交于点D,若∠D=36°,则∠CAB的度数为( )