
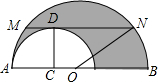
 如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,求阴影部分的面积.
如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,求阴影部分的面积. 分析 如图,作OE⊥MN于E.根据切线的性质得O1D为⊙O1的半径,易得四边形OO1DC为矩形,则OC=O1D,再根据垂径定理得到AC=BC=$\frac{1}{2}$MN,在Rt△OEN中,利用勾股定理得到ON2-OE2=EN2=$\frac{1}{4}$a2,然后利用阴影部分的面积=$\frac{1}{2}$S⊙C-$\frac{1}{2}$S⊙O进行计算.
解答 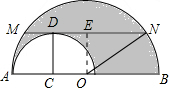 解:如图,
解:如图,
作OE⊥MN于E.
∵大半圆的弦AB与小半圆相切,
∴CD为⊙C的半径,
∴OC⊥MN,
又MN∥AB,
∴四边形DCOE为矩形,
∴OE=CD,
∵OE⊥MN,
∴ME=NE=$\frac{1}{2}$MN=$\frac{1}{2}$a,
在Rt△OEN中,ON2-OE2=EN2=$\frac{1}{4}$a2,
∴阴影部分的面积=$\frac{1}{2}$S⊙C-$\frac{1}{2}$S⊙O=$\frac{1}{2}$(π•ON2-π•CD2)=$\frac{1}{2}$π(ON2-OE2)=$\frac{π}{8}$a2.
点评 本题考查了圆的切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.


科目:初中数学 来源: 题型:解答题
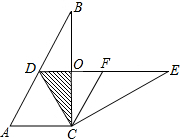 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上,DE交BC于点O.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上,DE交BC于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/千克) | 2 | 2.2 | 2.4 | 2.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1+x)2=2000 | B. | 2000(1+x)2=6600 | ||
| C. | (6600-200)(1+x)=6600 | D. | (6600-2000)(1+x)2=6600 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线y=kx+b交坐标轴于A(-4,0),B(0,3),则不等式kx+b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-4,0),B(0,3),则不等式kx+b<0的解集为( )| A. | x>3 | B. | -4<x<3 | C. | x>-4 | D. | x<-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com