
【题目】如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从点B出发,沿BC以2cm/s的速度向点C移动,点Q从点C出发,以1cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为t s,当t=时,△CPQ与△CBA相似.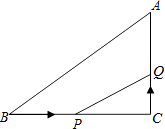
【答案】4.8或 ![]()
【解析】解:CP和CB是对应边时,△CPQ∽△CBA,
所以, ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得t=4.8;
CP和CA是对应边时,△CPQ∽△CAB,
所以, ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得t= ![]() .
.
综上所述,当t=4.8或 ![]() 时,△CPQ与△CBA相似.
时,△CPQ与△CBA相似.
所以答案是4.8或 ![]() .
.
【考点精析】利用勾股定理的概念和相似三角形的判定对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.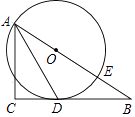
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将方格纸中的△ABC向上平移4个单位长度,然后向右平移6个单位长度,得到△A1B1C1.
(1)画出平移后的图形;
(2)线段AA1,BB1的位置关系是______;数量关系是________.
(3)如果每个方格的边长是1,那么△ABC的面积是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
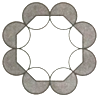
【题目】如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1 , 正八边形外侧八个扇形(阴影部分)面积之和为S2 , 则 ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P( ![]() +1,
+1, ![]() ﹣1)在双曲线y=
﹣1)在双曲线y= ![]() (x>0)上.
(x>0)上.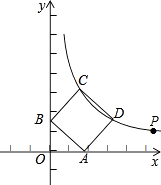
(1)求k的值;
(2)若正方形ABCD的顶点C,D在双曲线y= ![]() (x>0)上,顶点A,B分别在x轴和y轴的正半轴上,求点C的坐标.
(x>0)上,顶点A,B分别在x轴和y轴的正半轴上,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
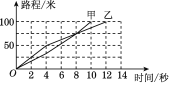
【题目】甲、乙两人进行比赛的路程与时间的关系如图所示.
(1)这是一场________米比赛;
(2)前一半赛程内________的速度较快,最终________赢得了比赛;
(3)两人第________秒在途中相遇,相遇时距终点________米;
(4)甲在前8秒的平均速度是多少?甲在整个赛程的平均速度是多少?乙在前8秒的平均速度是多少?乙在整个赛程的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图时用黑色的正六边形和白色的正方形按照一定的规律组合而成的两色图案

(1)当黑色的正六边形的块数为1时,有6块白色的正方形配套;当黑色的正六边形块数为2时,有11块白色的正方形配套;则当黑色的正六边形块数为3,10时,分别写出白色的正方形配套块数;
(2)当白色的正方形块数为201时,求黑色的正六边形的块数.
(3)组成白色的正方形的块数能否为100,如果能,求出黑色的正六边形的块数,如果不能,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com