
已知抛物线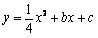 过点(-2,4),与y轴的交点为B(0,1)。 过点(-2,4),与y轴的交点为B(0,1)。(1)求抛物线的解析式及其顶点A的坐标; (2)在抛物线上是否存在一点C,使∠BAC=90。?若不存在说明理由;若存在,求出点C的坐标; (3)P、Q为抛物线上的两点,且横坐标分别为4和6,在x轴、y轴上分别有两个动点M、N,当PM +MN +NQ最小时,求出M、N两点的坐标。 |
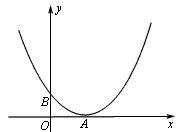 |
| 解:(1)∵ 抛物线过(- 2,4),(0,1) ∴ 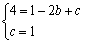 ∴ ∴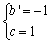 ∴抛物线的解析式为 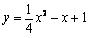 ,其顶点为(2,0) ,其顶点为(2,0)(2)假设存在C点使∠BAC = 90°, 设C(t, 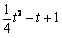 ), ),过C作CD⊥x轴于D,则D(t,0), ∴ 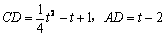 ∵ ∠BAC = 90°,∠ADC = 90° ∴ ∠BAO =∠ACD ∴ △BAO ∽△ACD ∴ 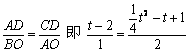 ∴解得t1 = 2(舍),t2 = 10 ∴ 存在C(10,16)使∠BAC = 90° (3)∵ 点P在抛物线上,且横坐标分别为4和6 ∴ P(4,1),Q(6,4) ∴ 点P关于x轴的对称点为P'(4,- 1), 点Q关于y轴的对称点Q'(- 6,4) ∵ 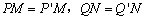 ∴ 当P'、M、N、Q'共线时, 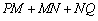 最小 最小∵ P'Q'的解析式为 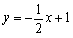 ∴ 此时M(2,0),N(0,1) |
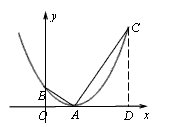 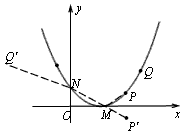 |


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
| A、y=x2-x-2 | B、y=-x2+x+2 | C、y=x2-x-2或y=-x2+x+2 | D、y=-x2-x-2或y=x2+x+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
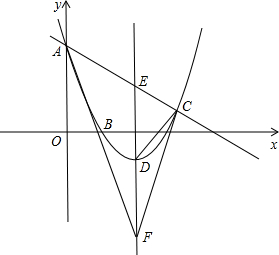 如图,已知抛物线过点A(0,6),B(2,0),C(7,
如图,已知抛物线过点A(0,6),B(2,0),C(7,| 5 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
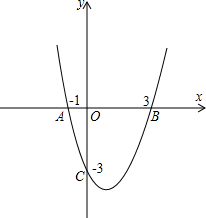 如图,已知抛物线过点A(-1,0)、B(3,0)、C(0,-3).
如图,已知抛物线过点A(-1,0)、B(3,0)、C(0,-3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com