
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() .则下列结论:①
.则下列结论:①![]() ;②
;②![]() ;③点
;③点![]() 是
是![]() 的中点.其中正确的是( )
的中点.其中正确的是( )

A.①②B.①③C.②③D.①②③
【答案】A
【解析】
根据“同弧所对圆周角相等”以及“等角的余角相等”即可解决问题①,运用相似三角形的判定定理证明△EBC∽△BDC即可得到②,运用反证法来判定③即可.
证明:①∵BC⊥AB于点B,
∴∠CBD+∠ABD=90°,
∵AB为直径,
∴∠ADB=90°,
∴∠BAD+∠ABD=90°,
∴∠CBD=∠BAD,
∵∠BAD=∠CEB,
∴∠CEB=∠CBD,
故①正确;
②∵∠C=∠C,∠CEB=∠CBD,
∴△EBC∽△BDC,
∴![]() ,
,
故②正确;
③∵∠ADB=90°,
∴∠BDF=90°,
∵DE为直径,
∴∠EBD=90°,
∴∠EBD=∠BDF,
∴DF∥BE,
假设点F是BC的中点,则点D是EC的中点,
∴ED=DC,
∵ED是直径,长度不变,而DC的长度是不定的,
∴DC不一定等于ED,
故③是错误的.
故选:A.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
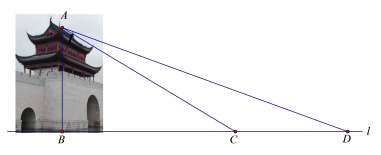
【题目】水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O为BC边上一点,⊙O经过A、B两点,与BC边交于点E,点F为BE下方半圆弧上一点,FE⊥AC,垂足为D,∠BEF=2∠F.

(1)求证:AC为⊙O切线.
(2)若AB=5,DF=4,求⊙O半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
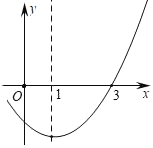
【题目】若二次函数y=x2﹣2x+k的部分图象如图所示,则关于x的一元二次方程x2﹣2x+k=0的解一个为x1=3,则方程x2﹣2x+k=0另一个解x2=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明本学期4次数学考试成绩如下表如示:
成绩类别 | 第一次月考 | 第二次月考 | 期中 | 期末 |
成绩分 | 138 | 142 | 140 | 138 |
(1)小明4次考试成绩的中位数为__________分,众数为______________分;
(2)学校规定:两次月考的平均成绩作为平时成绩,求小明本学期的平时成绩;
(3)如果本学期的总评成绩按照平时成绩占20%、期中成绩占30%、期末成绩占50%计算,那么小明本学期的数学总评成绩是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.

(1)试问坡AB的高BT为多少米?
(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米, ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(问题发现)
如图①,正方形AEFG的两边分别在正方形ABCD的边AB和AD上,连接CF.
填空:①线段CF与DG的数量关系为 ;
②直线CF与DG所夹锐角的度数为 .
(2)(拓展探究)
如图②,将正方形AEFG绕点A逆时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请利用图②进行说明.
(3(解决问题)
如图③,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=4,O为AC的中点.若点D在直线BC上运动,连接OE,则在点D的运动过程中,线段OE长的最小值为 (直接写出结果).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com