
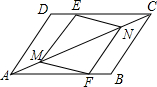
 如图,在平行四边形ABCD中,点M、N是对角线AC上的点,且AM=CN,DE=BF,求证:四边形MFNE是平行四边形.
如图,在平行四边形ABCD中,点M、N是对角线AC上的点,且AM=CN,DE=BF,求证:四边形MFNE是平行四边形. 分析 由平行四边形的性质得出AB=CD,AB∥CD,得出∠MAF=∠NCE,由SAS证明△AMF≌△CNE,得出对应边相等,对应角相等MF=NE,∠AMF=∠CNE,证出MF∥NE,即可得出结论.
解答 证明:∵四边形ABC是平行四边形,
∴AB=CD,AB∥CD,
∴∠MAF=∠NCE,
∵DE=BF,
∴AF=CE,
在△AMF和△CNE中,$\left\{\begin{array}{l}{AM=CN}&{\;}\\{∠MAF=∠NCE}&{\;}\\{AF=CE}&{\;}\end{array}\right.$,
∴△AMF≌△CNE(SAS),
∴MF=NE,∠AMF=∠CNE,
∴∠FMN=∠ENM,
∴MF∥NE,
∴四边形MFNE是平行四边形.
点评 本题考查了平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握平行四边形的判定与性质,并能进行推理论证是解决问题的关键.


科目:初中数学 来源: 题型:填空题
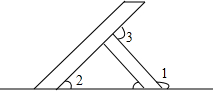 一天,爸爸带小明到建筑工地玩,他们看到一个如图所示的人字架,爸爸说:“小明,我考考你,这个人字架的夹角∠1等于140°,你知道∠3比∠2大多少吗?”小明马上得到了正确的答案,他的答案是40°.
一天,爸爸带小明到建筑工地玩,他们看到一个如图所示的人字架,爸爸说:“小明,我考考你,这个人字架的夹角∠1等于140°,你知道∠3比∠2大多少吗?”小明马上得到了正确的答案,他的答案是40°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | b | c | △ABC是否为直角三角形 |
| 4 | 3 | 5 | 是 |
| 6 | 8 | 10 | 是 |
| 8 | 15 | 17 | 是 |
| 10 | 24 | 26 | 是 |
| 12 | 35 | 37 | 是 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com