
【题目】如图所示,AB是⊙O的一条弦,DB切⊙O于点B,过点D作DC⊥OA于点C,DC与AB相交于点E.
(1)求证:DB=DE;
(2)若∠BDE=70°,求∠AOB的大小.

【答案】(1)证明见解析;(2)110°.
【解析】分析:(1)欲证明DB=DE,只要证明∠BED=∠ABD即可;
(2)因为△OAB是等腰三角形,属于只要求出∠OBA即可解决问题;
详解:(1)证明:∵DC⊥OA,
∴∠OAB+∠CEA=90°,
∵BD为切线,
∴OB⊥BD,
∴∠OBA+∠ABD=90°,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠CEA=∠ABD,
∵∠CEA=∠BED,
∴∠BED=∠ABD,
∴DE=DB.
(2)∵DE=DB,∠BDE=70°,
∴∠BED=∠ABD=55°,
∵BD为切线,
∴OB⊥BD,
∴∠OBA=35°,
∵OA=OB,
∴∠OBA=180°-2×35°=110°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像经过A(0,3),(
的图像经过A(0,3),(![]() ,
,![]() )两点.
)两点.
(1)求b、c的值.
(2)二次函数![]() 的图像与
的图像与![]() 轴是否有公共点?若有,求公共点的坐标,若没有,请说明情况.
轴是否有公共点?若有,求公共点的坐标,若没有,请说明情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM上的点,且MB=MN.

(1)求证:BN平分∠ABE;
(2)若BD=1,连结DN,当四边形DNBC为平行四边形时,求线段BC的长;
(3)如图②,若点F为AB的中点,连结FN、FM,求证:△MFN∽△BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
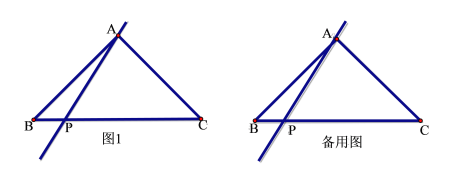
【题目】如图,△ABC中,![]() ,AB=AC,P是线段BC上一点,且
,AB=AC,P是线段BC上一点,且![]() .作点B关于直线AP的对称点D, 连结BD,CD,AD.
.作点B关于直线AP的对称点D, 连结BD,CD,AD.
(1)补全图形.
(2)设∠BAP的大小为α.求∠ADC的大小(用含α的代数式表示).
(3)延长CD与AP交于点E,直接用等式表示线段BD与DE之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=15,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且tanα=![]() 有以下的结论:① △ADE∽△ACD;② 当CD=9时,△ACD与△DBE全等;③ △BDE为直角三角形时,BD为12或
有以下的结论:① △ADE∽△ACD;② 当CD=9时,△ACD与△DBE全等;③ △BDE为直角三角形时,BD为12或![]() ;④ 0<BE≤
;④ 0<BE≤![]() ,其中正确的结论是___________(填入正确结论的序号)
,其中正确的结论是___________(填入正确结论的序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com