
【题目】如图,扇形AOB中,半径OA=2,∠AOB=120°,C是 ![]() 的中点,连接AC、BC,则图中阴影部分面积是( )
的中点,连接AC、BC,则图中阴影部分面积是( ) 
A.![]() ﹣2
﹣2 ![]()
B.![]() ﹣2
﹣2 ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为8cm2,AP垂直∠B的平分线BP于P,则△PBC的面积为( )
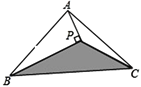
A. 3cm2 B. 4cm2 C. 5cm2 D. 6cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x、y的方程组![]() 的解为非负数.
的解为非负数.
(1)求a的取值范围;
(2)化简|2a+4|﹣|a﹣1|;
(3)在a的取值范围内,a为何整数时,使得2ax+3x<2a+3解集为x>1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,长方形ABCD中,AB=6cm,BC=4cm,E为CD的中点.点P从A点出发,沿A﹣B﹣C的方向在长方形边上匀速运动,速度为1cm/s,运动到C点停止.设点P运动的时间为ts.(图②为备用图)
(1)当P在AB上,t= s时,△APE的面积为长方形面积的![]() ;
;
(2)整个运动过程中,t为何值时,△APE为直角三角形?
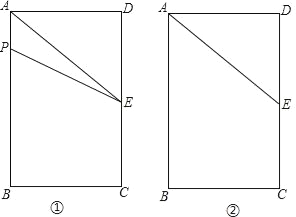
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于( ) 
A.55°
B.60°
C.65°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.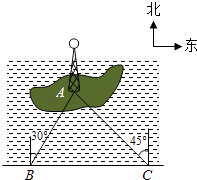
查看答案和解析>>
科目:初中数学 来源: 题型:
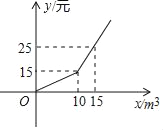
【题目】某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y元与每月用水量xm3之间的关系如图所示.
(1)求关于x的函数解析式;
(2)若某用户二、三月份共用水22m3(二月份用水量比三月份用水量多),缴纳水费共35元,则该用户二月份的用水量是多少m3?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角尺(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)若将图1中的三角尺绕点O以每秒5°的速度,沿顺时针方向旋转t秒,当OM恰好平分∠BOC时,如图2.
①求t值;
②试说明此时ON平分∠AOC;
(2)将图1中的三角尺绕点O顺时针旋转,设∠AON=α,∠COM=β,当ON在∠AOC内部时,试求α与β的数量关系;
(3)若将图1中的三角尺绕点O以每秒5°的速度沿顺时针方向旋转的同时,射线OC也绕点O以每秒8°的速度沿顺时针方向旋转,如图3,那么经过多长时间,射线OC第一次平分∠MON?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节前夕,小东的父母准备购买若干个粽子和咸鸭蛋(每个粽子的价格相同,每个咸鸭蛋的价格相同).已知粽子的价格比咸鸭蛋的价格贵1.8元,花30元购买粽子的个数与花12元购买咸鸭蛋的个数相同,求粽子与咸鸭蛋的价格各多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com