
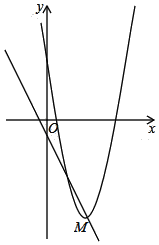
【题目】在平面直角坐标系中,抛物线![]() 的顶点M在直线L:
的顶点M在直线L:![]() 上.
上.
![]() 求直线L的函数表达式;
求直线L的函数表达式;
![]() 现将抛物线沿该直线L方向进行平移,平移后的抛物线的顶点为N,与x轴的右交点为C,连接NC,当
现将抛物线沿该直线L方向进行平移,平移后的抛物线的顶点为N,与x轴的右交点为C,连接NC,当![]() 时,求平移后的抛物线的解析式.
时,求平移后的抛物线的解析式.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
![]() 由题目已给出的抛物线一般式
由题目已给出的抛物线一般式![]() 直接化为顶点式
直接化为顶点式![]() 即可读出顶点坐标
即可读出顶点坐标![]() ,把顶点坐标代入直线L的解析式即可求出斜率
,把顶点坐标代入直线L的解析式即可求出斜率![]() ,进而写出直线L的解析式;
,进而写出直线L的解析式;
![]() 在直线L上取一点N,过N作
在直线L上取一点N,过N作![]() 轴于点E,构造
轴于点E,构造![]() 即
即![]() ,使得
,使得![]() ,则
,则![]() ,设平移后的二次函数的顶点式为
,设平移后的二次函数的顶点式为![]() ,则N点坐标为
,则N点坐标为![]() ,由
,由![]() 得,
得,![]() ,则C点坐标可以表示为
,则C点坐标可以表示为![]() ,又由N在直线L上,所以将N
,又由N在直线L上,所以将N![]() 代入
代入![]() 得,
得,![]() ,即平移后二次函数的顶点式可以为
,即平移后二次函数的顶点式可以为![]() ,把
,把![]() 代入其中,即可求出h’=3或 h’=-1,因为当对称轴在y轴左侧时抛物线与x轴无交点,与题意有又交点C不相符,则h’=-1应舍去,进而求得
代入其中,即可求出h’=3或 h’=-1,因为当对称轴在y轴左侧时抛物线与x轴无交点,与题意有又交点C不相符,则h’=-1应舍去,进而求得![]() 将h’和k’代入平移后二次函数的顶点式,再化为一般式即可.
将h’和k’代入平移后二次函数的顶点式,再化为一般式即可.
解:![]() 抛物线
抛物线![]()
所以![]() ,
,![]()
![]() 点的坐标为
点的坐标为![]()
又![]() 在直线L上
在直线L上
![]() 把
把![]() 代入
代入![]() 中得,
中得,![]()
解得,![]()
![]() 直线L的解析式为,
直线L的解析式为,![]()
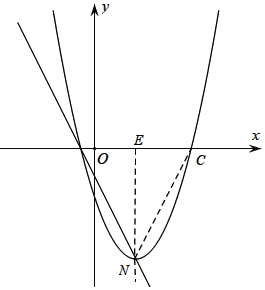
![]() 如图,设N(h′,k′),过N作
如图,设N(h′,k′),过N作![]() 轴于点E,连接NC.
轴于点E,连接NC.
由![]() 得,
得,![]() ,即
,即![]() .
.
![]() 点坐标为(h′-
点坐标为(h′-![]() k′,0)
k′,0)
又![]() 点N(h′,k′)在直线L上
点N(h′,k′)在直线L上
![]() 把N(h′,k′),代入
把N(h′,k′),代入![]() 得,k′=-2h′-2
得,k′=-2h′-2
设平移后的抛物线顶点式为y=![]() (x-h′)2+k′,
(x-h′)2+k′,
则把k′=-2h′-2代入上式得,y=![]() (x-h′)2-2h′-2
(x-h′)2-2h′-2
且h′-![]() k′=h′-
k′=h′-![]() (-2h′-2)=2h′+1
(-2h′-2)=2h′+1
∴C(2h′+1,0)
把C(2h′+1,0)代入y=![]() (x-h′)2-2h′-2得,
(x-h′)2-2h′-2得,
![]()
整理得,![]()
解得, h’=3或 h’=-1,
又![]() 当对称轴在y轴左边时抛物线与x轴无交点,这与题目已知条件“与x轴的右交点为C相矛盾
当对称轴在y轴左边时抛物线与x轴无交点,这与题目已知条件“与x轴的右交点为C相矛盾
∴h′=3,
k′=-2×3-2=-8
![]() 点坐标为
点坐标为![]()
![]() 平移后抛物线顶点式为,
平移后抛物线顶点式为,![]()
展开得,![]()


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+2交x轴于点A(﹣2,0)、B,交y轴于点C;
(1)求抛物线的解析式;
(2)点P从点A出发,以1个单位/秒的速度向终点B运动,同时点Q从点C出发,以相同的速度沿y轴正方向向上运动,运动的时间为t秒,当点P到达点B时,点Q也停止运动,设△PQC的面积为S,求S与t间的函数关系式并直接写出t的取值范围;
(3)在(2)的条件下,当点P在线段OB上时,设PQ交直线AC于点G,过P作PE⊥AC于点E,求EG的长.
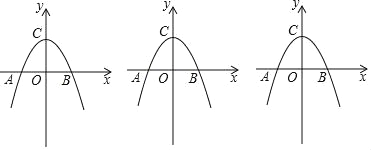
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0)与正比例函数y=kx、
(x>0)与正比例函数y=kx、 ![]() (k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
(k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点P是射线BA上的一个动点,以BP为半径的
,点P是射线BA上的一个动点,以BP为半径的![]() 交射线BC于点D,直线PD交直线AC于点E,点P关于直线AC的对称点为点
交射线BC于点D,直线PD交直线AC于点E,点P关于直线AC的对称点为点![]() ,连结
,连结![]() ,
,![]() ,设直线
,设直线![]() 与直线BC交于点F.
与直线BC交于点F.
![]() 当点P在线段BA上时,
当点P在线段BA上时,
![]() 求证:
求证:![]() ;
;
![]() 连结
连结![]() ,当
,当![]() 时,求
时,求![]() 的长;
的长;
![]() 连结AD,AF,当
连结AD,AF,当![]() 恰为等边三角形时,求此时四边形
恰为等边三角形时,求此时四边形![]() 的面积;
的面积;
![]() 当四边形
当四边形![]() 在
在![]() 内部时,请直接写出BP的取值范围.
内部时,请直接写出BP的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在距离大足城区的1.5公里的北山之上,有一处密如峰房的石窟造像点,今被称为北山石窟.北山石窟造像在两宋时期达到鼎盛,逐渐都成了以北山佛湾为中心,环绕营盘坡、佛耳岩,观音坡、多宝塔等多处造像点的大型石窟群.多宝塔,也称为“白塔”“北塔”,于岩石之上,为八角形阁式砖塔,外观可辨十二级,其内有八层楼阁,可沿着塔心内的梯道逐级而上,元且期间,小华和妈妈到大足北山游玩,小华站在坡度为l=1:2的山坡上的B点观看风景,恰好看到对面的多宝培,测得眼睛A看到塔顶C的仰角为30°,接着小华又向下走了10![]() 米,刚好到达坡底E,这时看到塔顶C的仰角为45°,若AB=1.5米,则多宝塔的高度CD约为( )(精确到0.1米,参考数据
米,刚好到达坡底E,这时看到塔顶C的仰角为45°,若AB=1.5米,则多宝塔的高度CD约为( )(精确到0.1米,参考数据![]() ≈1.732)
≈1.732)

A. 51.0米B. 52.5米C. 27.3米D. 28.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出的问题:只有一张电影票,小丽和小芳想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小丽和小芳都公平的方案.甲同学的方案:将红桃2、3、4、5四张牌背面向上,小丽先抽一张,小芳从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小丽看电影,否则小芳看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲同学的方案修改为只用2、3、5、7四张牌,抽取方式及规则不变,乙的方案公平吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() (
(![]() )的函数,表1中给出了几组
)的函数,表1中给出了几组![]() 与
与![]() 的对应值:
的对应值:
表1:
| … |
| 1 |
| 2 |
| 3 | … |
| … | 6 | 3 | 2 |
|
| 1 | … |

(1)以表中各对对应值为坐标,在图1的直角坐标系中描出各点,用光滑曲线顺次连接.由图像知,它是我们已经学过的哪类函数?求出函数解析式,并直接写出![]() 的值;
的值;
(2)如果一次函数图像与(1)中图像交于![]() 和
和![]() 两点,在第一、四象限内当
两点,在第一、四象限内当![]() 在什么范围时,一次函数的值小于(1)中函数的值?请直接写出答案.
在什么范围时,一次函数的值小于(1)中函数的值?请直接写出答案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com