
【题目】在一条笔直的公路上有A、B两地,甲从A地去B地,乙从B地去A地然后立即原路返回B地,返回时的速度是原来的2倍,如图是甲、乙两人离B地的距离y(千米)和时间x(小时)之间的函数图象. 
请根据图象回答下列问题:
(1)A、B两地的距离是千米,a=;
(2)求P的坐标,并解释它的实际意义;
(3)请直接写出当x取何值时,甲乙两人相距15千米.
【答案】
(1)90;2
(2)解:设甲离B地的距离y(千米)和时间x(小时)之间的函数关系式为y=kx+b,乙离B地的距离y(千米)和时间x(小时)之间的函数关系式为y=mx+n,
将(0,90)、(3,0)代入y=kx+b中,
![]() ,解得:
,解得: ![]() ,
,
∴甲离B地的距离y和时间x之间的函数关系式为y=﹣30+90;
将(0,0)、(2,90)代入y=mx+n中,
![]() ,解得:
,解得: ![]() ,
,
∴此时y=45x(0≤x≤2);
将(2,90)、(3,0)代入y=mx+n中,
![]() ,解得:
,解得: ![]() ,
,
此时y=﹣90x+270(2≤x≤3).
∴乙离B地的距离y和时间x之间的函数关系式为y= ![]() .
.
令y=﹣30+90=45x,解得:x=1.2,
当x=1.2时,y=45x=45×1.2=54,
∴点P的坐标为(1.2,54).
点P的实际意义是:甲、乙分别从A、B两地出发,经过1.2小时相遇,这时离B地的距离为54千米
(3)解:当0≤x<1.2时,﹣30x+90﹣45x=15,
解得:x=1;
当1.2≤x<2时,45x﹣(﹣30x+90)=15,
解得:x=1.4;
当2≤x≤3时,﹣90x+270﹣(﹣30x+90)=15,
解得:x=2.75.
综上所述:当x为1、1.4或2.75时,甲乙两人相距15千米
【解析】解:(1)观察函数图象可知:A、B两地的距离是90千米, ∵乙从B地去A地然后立即原路返回B地,返回时的速度是原来的2倍,
∴a=3× ![]() =2.
=2.
故答案为:90;2.
(1)观察函数图象即可得出A、B两地的距离,由乙往返需要3小时结合返回时的速度是原来的2倍,即可求出a值;(2)观察函数图象找出点的坐标,利用待定系数法求出甲、乙离B地的距离y和时间x之间的函数关系式,令两函数关系式相等即可求出点P的坐标,再解释出它的实际意义即可;(3)分0≤x<1.2、1.2≤x<2和2≤x≤3三段,找出关于x的一元一次方程,解之即可得出结论.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上,则a的值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地保护环境,某区污水处理厂决定购买A,B两种型号污水处理设备10台,其中每台的价格、月处理污水量如下表.已知购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.

(1)求a,b的值;
(2)某区污水处理厂决定购买污水处理设备的资金既不少于108万元也不超过110万元,问有几种购买方案?每月最多能处理污水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
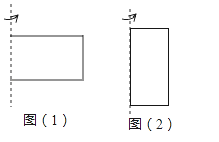
【题目】如图,长方形的长和宽分别是7cm和3cm,分别绕着它的长和宽所在的直线旋转一周,回答下列问题:
(1)如图(1),绕着它的宽所在的直线旋转一周,所得到的是什么样的几何体?得到的几何体的体积是多少?(π取3.14)
(2)如图(2),绕着它的长所在的直线旋转一周,所得到的是什么样的几何体?得到的几何体的体积是多少?(π取3.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别以□ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形,△ABE,△CDG,△ADF.
(1)如图1,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF.请判断GF与EF的关系(只写结论,不需证明);
(2)如图2,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,给出证明;若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: ![]() ,
, ![]() ,结果保留整数.)
,结果保留整数.)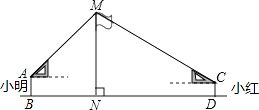
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com